Conjuntos clásicos de números
Contents
1.1. Conjuntos clásicos de números#
1.1.1. Números naturales, \(\mathbb{N}\)#
El conjunto más pequeño de números es el formado por los números naturales,
Hay distintas opiniones acerca de si se debe incluir el \(0\) en este conjunto o no. De todos modos, esto es indiferente para nuestro objetivo.
1.1.2. Números enteros, \(\mathbb{Z}\)#
Cuando los naturales se mostraron insuficientes para algunas operaciones sencillas (como la resta) el conjunto fue ampliado y surgieron los números enteros,
Es evidente que \(\mathbb{N}\subset\mathbb{Z}\).
1.1.3. Números racionales, \(\mathbb{Q}\)#
Al estudiarse la división fue evidente que con los números enteros no era suficiente, así que nació el conjunto de números racionales, \(\mathbb{Q}\). Este conjunto está formado por las fracciones, \(\frac{p}{q}\), donde \(p\) es entero y \(q\) natural (evitamos así la división entre \(0\)).
Una representación aproximada (y, por lo tanto, siempre menos precisa) de representar los racionales es en formato decimal: \(\alpha_0\, .a_1 a_2... a_n...\), donde \(\alpha_0\in\mathbb{Z}\) y \(a_i\in\mathbb{Z}\) con \(0\leq a_i\leq 9\), para cualquier índice \(i\).
Si pensamos que \(p=\frac{p}{1}\), \(\forall p\in\mathbb{Z}\), resulta que \(\mathbb{Z}\subset\mathbb{Q}\).
1.1.4. Números reales, \(\mathbb{R}\)#
Durante muchos siglos se pensó que era suficiente con los números racionales, pese a que las evidencias mostraban lo contrario. Finalmente, los griegos tuvieron que rendirse a las pruebas que mostraban que, por ejemplo, la longitud de la hipotenusa de un triángulo rectángulo con las dos aristas de longitud unidad, no puede ser representada como fracción. Es decir, que \(\sqrt{2}\not\in\mathbb{Q}\). Es un ejemplo de número irracional, como también lo son \(\pi\), \(e\), \(\sqrt{3}\), etc.. Aparecen los números reales, \(\mathbb{R}\), que agrupan tanto a los racionales como a los irracionales.
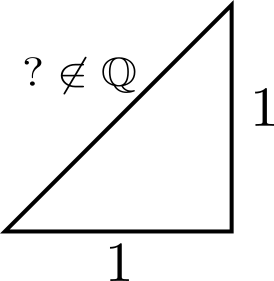
Hay dos propiedades muy importantes de los números reales que nos gustaría destacar aquí:
Propiedad arquimediana: Dados dos números reales, \(a,b\in\mathbb{R}\), tales que \(0<a<b\), entonces \(\exists n\in\mathbb{N}\) tal que \(b<na\).
Por ejemplo, si \(a=0.1\) y \(b=6000.38\), podemos tomar \(n=100000\) para obtener que \(6000.38<100000*0.1\).
Propiedad. Densidad de \(\mathbb{Q}\) en \(\mathbb{R}\): Dados dos números reales \(a\) y \(b\), con \(a<b\), existe \(q\in\mathbb{Q}\) tal que \(a<q<b\).
Estas propiedades merecen una breve explicación:
La propiedad arquimediana viene a decirnos que dado cualquier número real siempre podremos encontrar otro más grande y, multiplicando el razonamiento por \(-1\), que también podremos encontrar otro más pequeño. Es decir, que \(\mathbb{R}\) es un conjunto infinito tanto por arriba como por abajo.
La propiedad de densidad indica que dados dos números reales cualesquiera (y distintos, claro) siempre habrá otro número real entre ellos. Y otros dos números reales entre estos tres y… Es decir, que el conjunto de números reales es continuo.
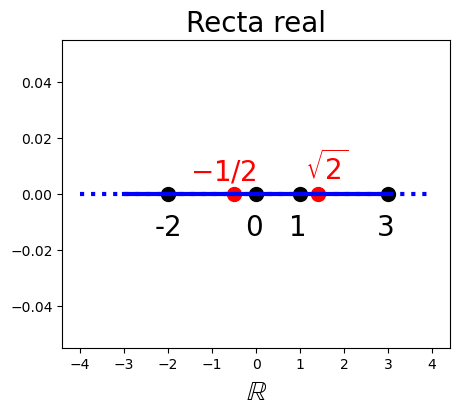
Con esto ya tenemos la justificación teórica que necesitamos para introducir la forma más común de representar los números reales: en una recta infinita. Dado un punto de la recta, \(a\), que podemos identificar con un número real, a su derecha estarán los números reales mayores que \(a\) y a su izquierda los menores. Y la recta no presenta agujeros gracias a la propiedad de densidad.
Veamos algunas definiciones importantes que tienen que ver con la acotación de subconjuntos de \(\mathbb{R}\).
Definición: Sea \(\mathrm{A}\) un subconjunto no vacío de \(\mathbb{R}\) (\(\mathrm{A}\subset\mathbb{R}\), \(\mathrm{A}\not=\emptyset\)).
Decimos que \(M\in\mathbb{R}\) es cota superior de \(\mathrm{A}\) si
\[\begin{equation*} x\leq M,\qquad\forall x\in\mathrm{A}. \end{equation*}\]Si el conjunto \(\mathrm{A}\) admite alguna cota superior decimos que está acotado superiormente.
Decimos que \(m\in\mathbb{R}\) es cota inferior de \(\mathrm{A}\) si
\[\begin{equation*} m\leq x,\qquad\forall x\in\mathrm{A}. \end{equation*}\]Si el conjunto \(\mathrm{A}\) admite alguna cota inferior decimos que está acotado inferiormente.
Si \(\mathrm{A}\) está acotado superior e inferiormente diremos simplemente que está acotado.
