Convexidad y concavidad
Contents
3.5. Convexidad y concavidad#
3.5.1. Definiciones#
Matemáticamente, la idea de una función convexa es sencilla: es aquella función en la que la recta secante está por encima de la gráfica de la función. Dicho de forma coloquial: es un vaso en el que no se derramaría el agua.
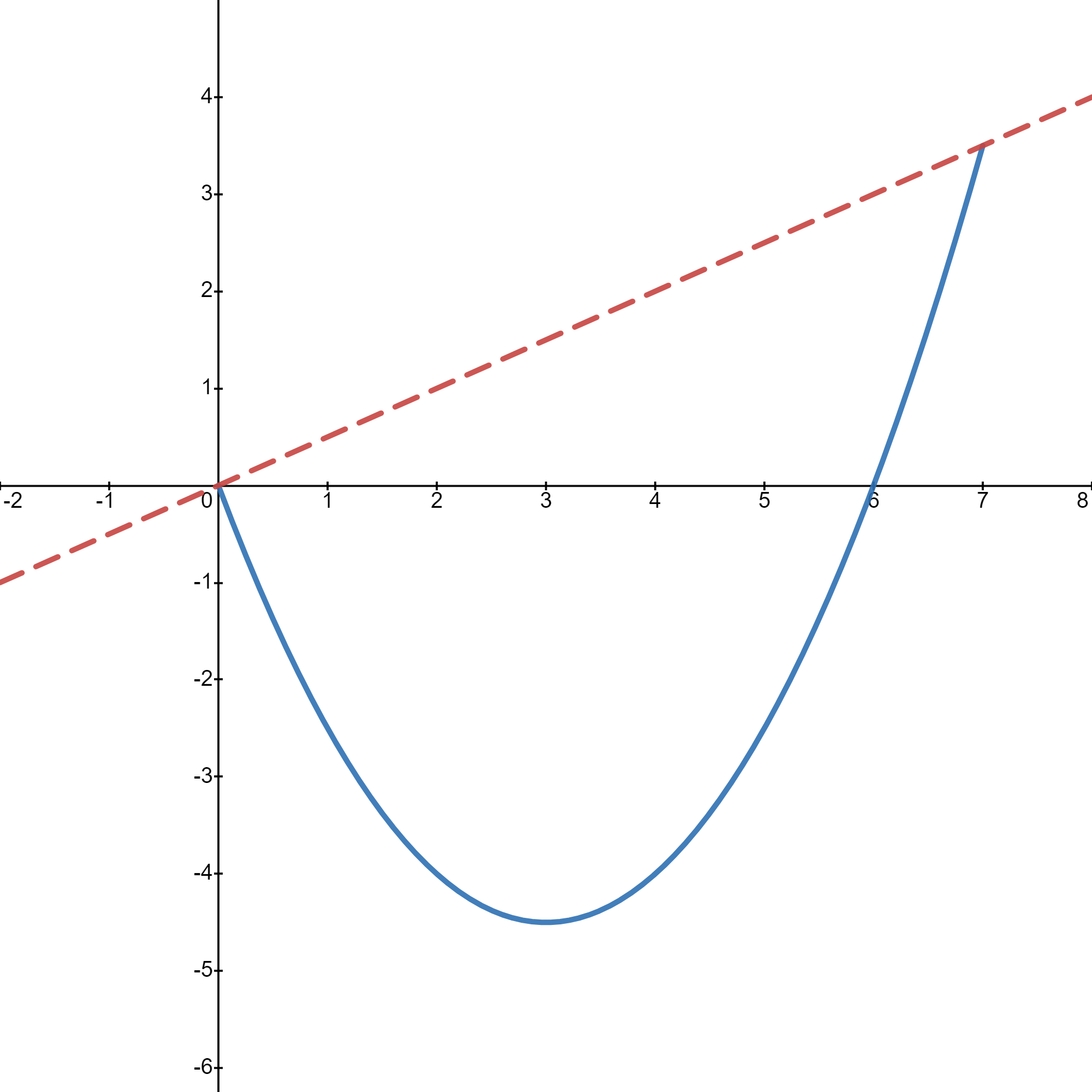
Si recordamos que la recta secante a \(f\) por \(a\) y \(b\) tiene ecuación \(r(x) =\frac{f(b)-f(a)}{b-a}(x-a) + f(a)\), obtenemos la siguiente definición formal:
Definition (Convexidad)
Se dice que \(f\) es convexa en \([a,b]\) si
Análogamente, diremos que \(f\) es cóncava si la gráfica queda por debajo de la recta secante o, equivalentemente, si su inversa es una función convexa.
Definition (Concavidad)
Se dice que \(f\) es cóncava en \([a,b]\) si \(-f\) es convexa en ese intervalo.
La última definición vinculada a concavidad/convexidad es la siguiente:
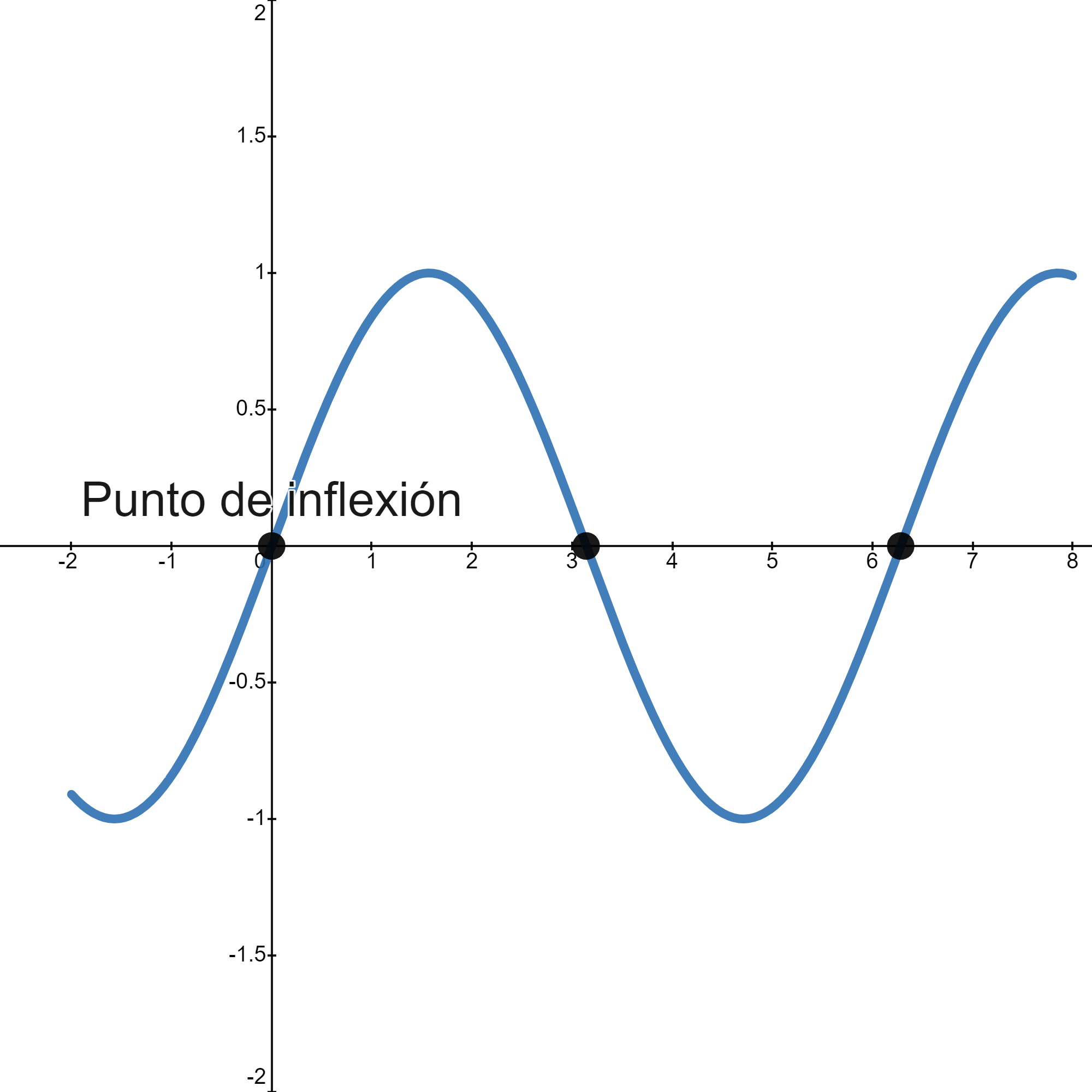
Definition (Punto de inflexión)
Se dice que \(f\) tiene un punto de inflexión en \(x_{0}\) si en ese punto la función pasa de cóncava a convexa o viceversa.
3.5.2. Convexidad y concavidad para funciones suficientemente derivables#
Y ahora una reflexión, que nos llevará a una importante propiedad: si una función es convexa (mira el gráfico del principio de esta sección), su derivada, si existe, será negativa al principio, luego valdrá \(0\) en el mínimo relativo para pasar a ser positiva a continuación. Es decir, la derivada de una función convexa es creciente. Y, por tanto, la derivada de ésta (es decir, la segunda derivada de \(f\), siempre que exista) será positiva. Por supuesto, pasa lo contrario para una función cóncava.
Todo esto se resume en la siguiente
Property
Sea \(f:[a,b] \longrightarrow \mathbb{R}\) continua en \([a,b]\) y derivable en \((a,b)\). Entonces \(f\) es convexa en \([a,b]\) si y sólo si \(f'\) es creciente en \((a,b)\). Esto equivale a que \(f'' \geq 0\), si \(f\) tiene derivada segunda.
Análogamente, \(f\) es cóncava en \([a,b]\) si y sólo si \(f'\) es decreciente en \((a,b)\) (es decir, si y sólo si \(f'' \leq 0\), en caso de existir derivada segunda).
Ilustramos esta propiedad en la siguiente figura:
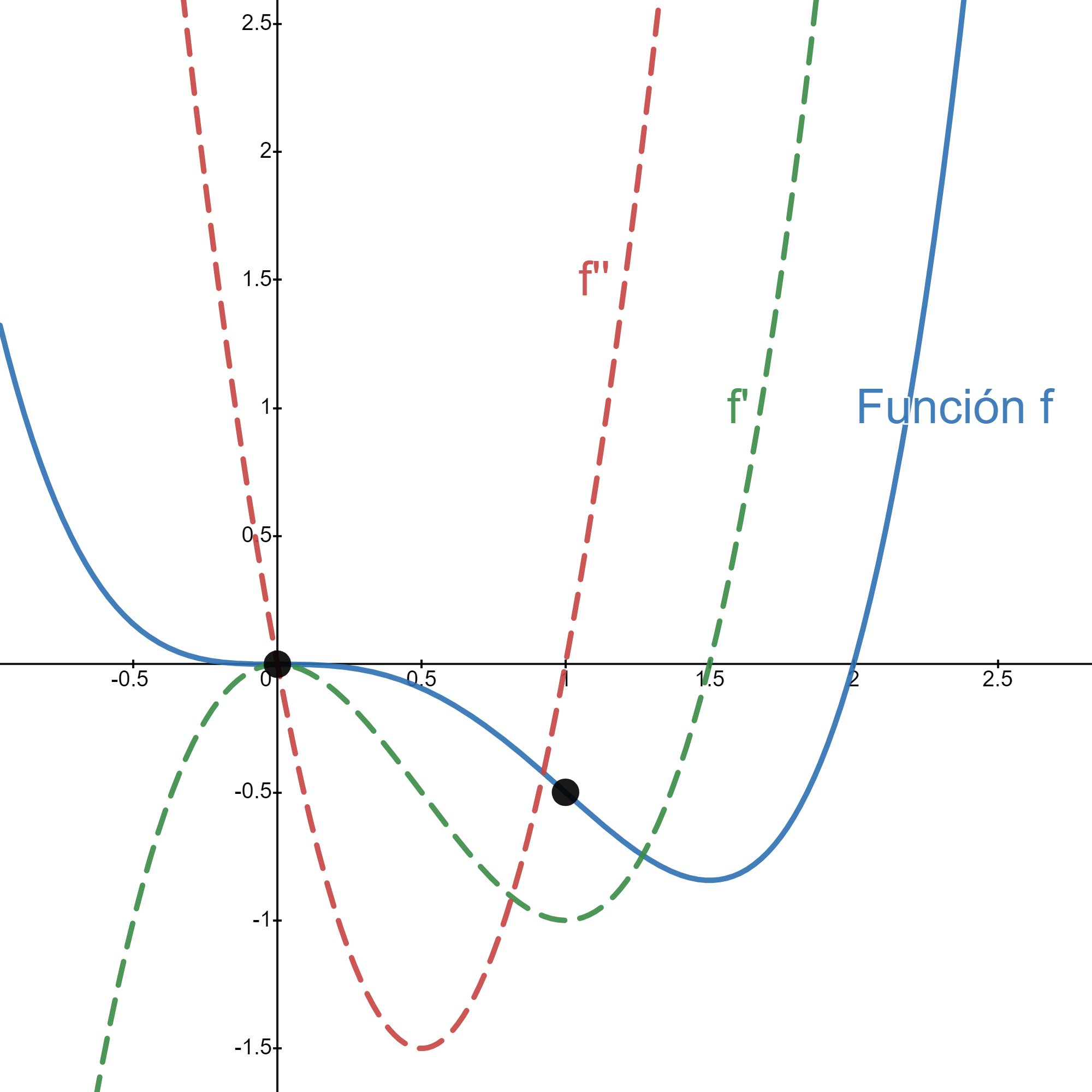
3.5.3. Más información#
En esta página web puedes ver más explicaciones y algunos ejemplos (tanto resueltos como propuestos): https://www.funciones.xyz/concavidad-y-convexidad-de-una-funcion-curvatura/
En la wiki empiezan fácil, pero van hacia conceptos más abstractos. Aún así, puedes echarle un vistazo: https://es.wikipedia.org/wiki/Función_convexa

