Definiciones básicas
Contents
2.2. Definiciones básicas#
Definición: Sea \(\mathrm{A}\subset\mathbb{R}\). Definimos función real de variable real a una aplicación que lleva cada punto de \(\mathrm{A}\) en un único punto de \(\mathbb{R}\).
Definición: Sea una función \(f:\mathrm{A}\subset\mathbb{R}\rightarrow\mathbb{R}\). Entonces:
El dominio de \(f\) es el conjunto \(\mathrm{A}\).
La imagen de \(f\) es el conjunto \( \displaystyle \mathrm{im}\, f=\left\{y\in\mathbb{R}: \exists x\in \mathrm{dom}\, f \text{ tal que }f(x)=y\right\}\).
Diremos que \(f\) es acotada en \(\mathrm{A}\) (resp., acotada superior o inferiormente) si el conjunto \(\mathrm{im}\, f\) es acotado (resp., acotado superior o inferiormente).
Sea \(\mathrm{B}\subset\mathrm{A}\). Diremos que \(f\) es creciente en \(\mathrm{B}\) si \( \displaystyle \forall x_1, x_2\in\mathrm{B} / x_1<x_2\Rightarrow f(x_1)\leq f(x_2)\).
Sea \(\mathrm{B}\subset\mathrm{A}\). Diremos que \(f\) es estrictamente creciente en \(\mathrm{B}\) si \( \displaystyle \forall x_1, x_2\in\mathrm{B} / x_1<x_2\Rightarrow f(x_1)< f(x_2)\).
Sea \(\mathrm{B}\subset\mathrm{A}\). Diremos que \(f\) es decreciente en \(\mathrm{B}\) si \( \displaystyle \forall x_1, x_2\in\mathrm{B} / x_1<x_2\Rightarrow f(x_1)\geq f(x_2)\).
Sea \(\mathrm{B}\subset\mathrm{A}\). Diremos que \(f\) es estrictamente decreciente en \(\mathrm{B}\) si \( \displaystyle \forall x_1, x_2\in\mathrm{B} / x_1<x_2\Rightarrow f(x_1)> f(x_2)\).

2.2.1. Simetrías par/impar#
Definición: Sea \(f:\mathbb{R}\rightarrow\mathbb{R}\). Diremos que \(f\) es
Par si \(f(x)=f(-x)\), \(\forall x\in\mathbb{R}\).
Impar si \(f(x)=-f(-x)\), \(\forall x\in\mathbb{R}\).
El nombre proviene de los monomios fundamentales. Los monomios con exponente par (\(x^2\), \(x^4\), \(x^6\),…) tienen simetría par y los monomios con exponente impar (\(x\), \(x^3\), \(x^5\),…) tienen simetría impar.
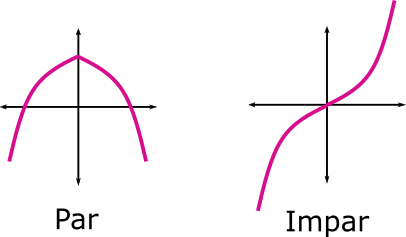
2.2.2. Función periódica#
Definición: Sea \(f:\mathbb{R}\rightarrow\mathbb{R}\). Diremos que \(f\) es periódica, con período \(T\) si
El ejemplo más clásico de funciones periódicas son las funciones trigonométricas. Por ejemplo, la función seno es periódica con un período de \(2\pi\), como mostraremos en la siguiente sección.
Si sabemos que una función tiene un período \(T\) nos será suficiente con representarla en \([0,T]\). Después se repetirá.
2.2.3. Composición de funciones#
Definición: Sean \(f:\mathrm{A}\subset\mathbb{R}\rightarrow\mathbb{R}\), \(g:\mathrm{B}\subset\mathbb{R}\rightarrow\mathbb{R}\), con \(f(\mathrm{A})\subset\mathrm{B}\). Definimos la función compuesta \(g\circ f\) (se lee f compuesta con g) a la función
Ejercicios
Componer, de las dos formas posibles, las funciones \(f(x)=e^{x^2-1}\) y \(g(x)=\sin(2x)+\cos(x)\).
Solución: \(\displaystyle\left(g\circ f\right)(x)=g\left(f(x)\right) = g\left(e^{x^2-1}\right)= \sin\left(2e^{x^2-1}\right) +\cos\left(e^{x^2-1}\right)\).
Notemos que la composición no es una operación conmutativa. En este mismo ejemplo, si hacemos la composición al revés,
\(\displaystyle \left(f\circ g\right)(x) = f\left(g(x)\right) = f\left(\sin(2x)+\cos(x)\right) = e^{\left(\sin(2x)+\cos(x)\right)^2-1}\).
Componer, de las dos formas posibles, las funciones \(f(x)=\frac{x^4+x^2}{5}\), \(g(x)=\ln(x+2)\).
2.2.4. Función inversa#
Definición: Sea \(f:\mathrm{A}\subset\mathbb{R}\rightarrow\mathbb{R}\) una función inyectiva (es decir, si \(x\not= y\), \(f(x)\not= f(y)\)). Entonces existe una única función \(h:\mathrm{im}\, f\rightarrow\mathbb{R}\) tal que \(h\left(f(x)\right)=x\), \(\forall x\in\mathrm{A}\).
Esta función se denomina inversa de \(f\) y suele denotarse como \(f^{-1}\).
Es decir, según la definición de inversa, tenemos que \(f^{-1}\circ f=\mathrm{Id}\). Además, en este caso se verifica que la composición es conmutativa, es decir, que \(f\circ f^{-1}=\mathrm{Id}\) (la función \(\mathrm{Id}\) es la función identidad, es decir, \(\mathrm{Id}(x)=x\), \(\forall x\in\mathbb{R}\)).

¡No se debe pensar que \(\boldsymbol{f^{-1}=\frac{1}{f}}\)!
La forma práctica de calcular una función inversa es despejar la \(x\) en función de la \(y\) (es decir, de \(f(x)\)) e intercambiar sus papeles. Vemos un ejemplo en el siguiente ejercicio.
Ejercicios
Calcular la inversa de la función \(\displaystyle f(x)=\frac{e^x}{1+e^x}\).
Solución:
\[\frac{e^x}{1+e^x}=y\Rightarrow e^x=y+ye^x\Rightarrow e^x(1-y)=y \Rightarrow e^x=\frac{y}{1-y}\Rightarrow x=\ln\left(\frac{y}{1-y}\right). \]Entonces la función inversa será \(\displaystyle f^{-1}(x)=\ln\left(\frac{x}{1-x}\right)\).
Queda como ejercicio que el lector compruebe que efectivamente \(f^{-1}\circ f=f\circ f^{-1}=\mathrm{Id}\).
Nota: Tanto \(\log\) como \(\mathrm{ln}\) representan para nosotros el logaritmo neperiano.
Calcular la inversa de la función \(\displaystyle f(x)=\frac{2}{1+e^x}\).
