5.5. Derivación en Python#

En esta sección aprenderemos a derivar con Sympy y aplicaremos este conocimiento sobre algunos ejemplos del Polinomio de Taylor.

5.5.1. Derivar en Sympy#

Para calcular simbólicamente la derivada primera de una función mediante Sympy se emplea la función diff. Por ejemplo

import sympy as sp
x=sp.symbols('x')
f=sp.exp(x)*sp.cos(x)
d1f=sp.diff(f,x)
print('La derivada primera es: ',d1f)

La derivada primera es:  -exp(x)*sin(x) + exp(x)*cos(x)

Para calcular la derivada i-ésima

import sympy as sp
x=sp.symbols('x')
f=sp.exp(x)*sp.cos(x)
d2f=sp.diff(f,x,2)
print('La derivada segunda es: ',d2f)
d3f=sp.diff(f,x,3)
print('La derivada tercera es: ',d3f)

La derivada segunda es:  -2*exp(x)*sin(x)
La derivada tercera es:  -2*(sin(x) + cos(x))*exp(x)

5.5.2. Uso de sp.lambdify#

En el resto de esta práctica, así como en el resto del curso, necesitaremos que una función simbólica de Sympy actúe sobre variables que almacenen números en coma flotante o arrays de Numpy. En concreto, y aunque las utilidades de este comando son mucho más amplias, lo necesitaremos para representar las funciones obtenidas en Matplotlib.

Esto se consigue utilizando la función sp.lambdify.

Mostramos a continuación, sobre un ejemplo, su uso. En él denotaremos f la función en Sympy y fn la función numérica generada a partir de ésta con sp.lambdify.

import sympy as sp
import numpy as np
x=sp.symbols('x')
# La funcion f es simbolica: no podemos evaluarla
# en variables numericas que almacenen valores en coma flotante, 
# o en arrays de numpy
f=sp.sin(x)*sp.exp(x)
# La funcion fn es numerica, y podemos evaluarla en numeros en coma flotante o en arrays de Numpy
fn=sp.lambdify(x,f)
x=np.linspace(-np.pi,np.pi,5)
print(fn(x))

[-5.29217867e-18 -2.07879576e-01  0.00000000e+00  4.81047738e+00
  2.83391752e-15]

5.5.3. Ejercicio 1: polinomio de Taylor#

El objetivo de este ejercicio es programar la función series de Sympy, que sirve para calcular el polinomio de Taylor.

El objetivo es escribir una función Python que calcule de forma simbólica el polinomio de Taylor de una función dada. Como argumentos de entrada debe recibir la función, \(f\), el centro de Taylor, \(x_{0}\), y el orden del polinomio, \(n\).

La función debe devolver el polinomio de Taylor y la función que proporciona el resto de Taylor.

# Codigo aqui

import sympy as sp

x,t=sp.symbols('x,t')

# p: polinomio de Taylor
# R: resto en valor absoluto
def taylor(f,x0,n):
    p=0
    for i in range(n+1):
        p+=sp.diff(f,x,i).subs(x,x0)/sp.factorial(i)*(x-x0)**i
    R=sp.diff(f,x,n+1).subs(x,t)/sp.factorial(n+1)*(x-x0)**(n+1)
    return p,R

Ahora vamos a emplear la función anterior para calcular el polinomio de Taylor de grado 5 de la función

\[f(x)=\sin(x)-\cos(x),\]

centrado en \(x_0=0\).

# Codigo aqui
import sympy as sp
x=sp.symbols('x')
f=sp.sin(x)-sp.cos(x)
p,R=taylor(f,0,5)
print('Polinomio de Taylor: \n',p,'\n\n Resto de Taylor: \n',R)

Polinomio de Taylor: 
 x**5/120 - x**4/24 - x**3/6 + x**2/2 + x - 1 

 Resto de Taylor: 
 x**6*(-sin(t)/720 + cos(t)/720)

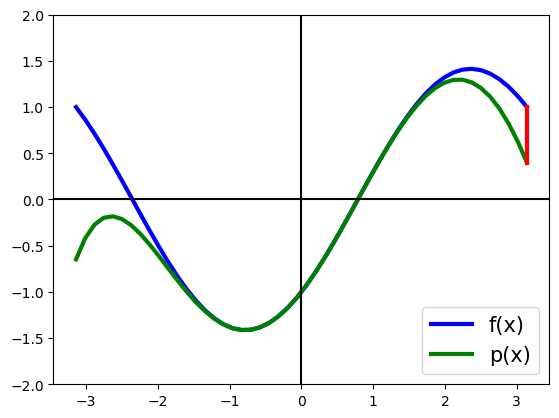
A continuación vamos a representar, empleando Matplotlib, la función f junto a su polinomio de Taylor, p.

También aproximaremos el valor de \(f(\pi)\) mediante dicho polinomio de Taylor y representaremos (mediante un segmento en rojo) la diferencia entre el valor exacto y el aproximado mediante el polinomio de Taylor.

Representación de la función, el polinomio de Taylor y el residuo

# Codigo aqui
import numpy as np
import matplotlib.pyplot as plt
x=sp.symbols('x')
fn=sp.lambdify(x,f)
pn=sp.lambdify(x,p)
x=np.linspace(-np.pi,np.pi)
plt.plot(x,fn(x),label='f(x)', lw='3',c='b')
plt.plot(x,pn(x),label='p(x)', lw='3',c='g')
plt.plot([np.pi,np.pi],[fn(np.pi),pn(np.pi)],lw='3',c='r')
plt.axhline(0,color='k')
plt.axvline(0,color='k')
plt.ylim(-2,2)
plt.legend(loc='lower right',fontsize=15)
plt.show()
../../_images/05.Derivacion_12_0.png

Ahora vamos a calcular el valor absoluto del resto de Taylor:

\[ |R(x)|=|f(x)-p_n(x)| \]

así como la estimación (cota superior), a partir de la fórmula del resto que nos proporciona el Teorema de Taylor:

\[ |R(x)|\leq \max_{t \in [0,x]} \dfrac{|f^{n+1}(t)|}{(n+1)!}|x-0|^{n+1}. \]

Para calcular la cota superior del resto de Taylor, debemos acotar la función \(g(t)=\dfrac{|f^{n+1}(t)|}{(n+1)!}|x-0|^{n+1}\) para \(x=\pi\), en el intervalo correspondiente.

Vamos a realizar esta acotación haciendo algo de trampa: utilizaremos Scipy. Concretamente su función optimize.fminbound, que calcula el mínimo de una función real de variable real en un intervalo.

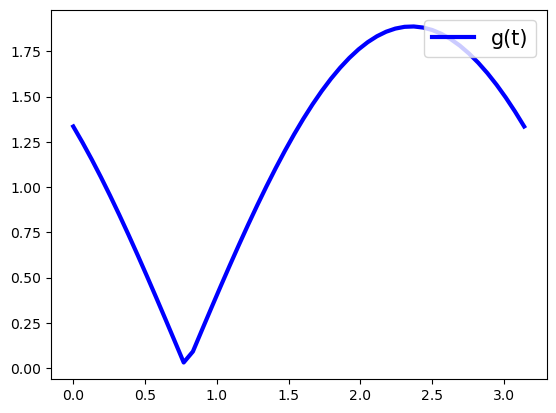
También haremos esta acotación gráficamente: representaremos la gráfica de \(g\) (el valor absoluto del resto de Taylor) en función de \(t\in[0,\pi]\) y buscaremos su máximo.

from scipy import optimize
import numpy as np
x=sp.symbols('x')

# Convertir el resto de Taylor para x=pi en una funcion numerica
# Como buscamos el maximo, multiplicamos por -1 (maximizar es minimizar el opuesto)
Rn=sp.lambdify(t,-sp.Abs(R.subs(x,sp.pi))) # Opuesto del resto
x=np.linspace(0,np.pi)
# Solucion grafica
plt.plot(x,-Rn(x),label='g(t)', lw='3',c='b')
plt.legend(loc='upper right',fontsize=15)
plt.show()
# Optimizamos el resto de Taylor
topt=optimize.fminbound(Rn, 0,np.pi)

print('El error es menor o igual que: ',-Rn(topt))
print('El error real es: ',np.abs(fn(np.pi)-pn(np.pi)))
../../_images/05.Derivacion_14_0.png 
El error es menor o igual que:  1.8883467170460109
El error real es:  0.5998660124549196

5.5.4. Ejercicio 2: máximos#

Dado un canal de sección trapezoidal de lado 2, calcular el ángulo \(\alpha\) (ver dibujo) que maximiza el área de la sección del canal.

../../_images/cap5_canal.svg

  1. A mano. Obtener la función que proporciona el área del canal en función del ángulo \( \alpha \)

  2. Simbólicamente: con Sympy.

  3. Numéricamente mediante el método de Newton con error menor que \( 10^{-4} \).

# 2. Resolvemos el problema utilizando Sympy
x,xn=sp.symbols('x,xn')
# Funcion que describe el area de la seccion en funcion del angulo
f=4*sp.sin(x)*(1+sp.cos(x))
d1f=sp.diff(f,x)
d1fn=sp.lambdify(x,d1f)
alphamax=sp.solve(d1f)
print('La sección máxima se alcanza con ángulo: ',float(alphamax[1]))

La sección máxima se alcanza con ángulo:  1.0471975511965979

# 3. Aproximamos el máximo con el método de Newton
maxit=100
eps=1e-4
d2fn=sp.diff(d1f,x)
d2fn=sp.lambdify(x,d2f)
xn=np.pi/2
for i in range(0,maxit):
    res=d1fn(xn)/d2fn(xn)
    xn=xn-res
    if (np.abs(res)<eps):
        break
print('La sección máxima se alcanza con ángulo: ',xn)

La sección máxima se alcanza con ángulo:  0.9650678568332388