1.2. Números complejos

Durante muchos siglos se pensó que con los números reales era suficiente. Que ahí estaba todo. Ecuaciones como

\[ x^2+1=0 \]

simplemente no tenían solución. Hasta que por diversos motivos empezó a ser importante tener un marco para su resolución. Aparecen los números complejos, \(\mathbb{C}\).

Nota: Si te pica la curiosidad, puedes mirar algo sobre la historia de los números complejos en la web del matemático canario Rodrigo Trujillo: https://rotrujil.webs.ull.es/WebAMVI/HISTORIA.pdf

Voviendo a nuestra introducción a \(\mathbb{C}\), es necesario continuar la cadena de inclusiones, es decir, como ya tenemos

\[ \mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}, \]

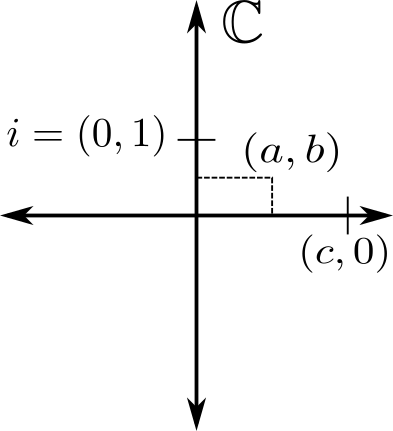
se debe imponer \(\mathbb{R}\subset\mathbb{C}\). Como, debido a la propiedad arquimediana, ya no caben más números en la recta real, la forma geométrica más natural de ampliar los números es pasar al plano. Entonces, la primera idea de números complejos debe ser la idea geométrica del plano, lo que se conoce como plano complejo:

\[ \mathbb{C}=\left\{(a,b) / a,b\in\mathbb{R}\right\}. \]

Dentro del plano complejo los números reales se identifican con el eje de abscisas. Entonces el número real \(a\) corresponde al complejo \((a,0)\).

1.2.1. Representación cartesiana

Estamos escribiendo los números complejos como pares de números reales. Ésta es la representación cartesiana.

Por supuesto, no basta con tener un conjunto de números. Es necesario saber operar con ellos. Introducimos dos operaciones, la suma y la multiplicación, como sigue:

• \((a,b)+(c,d):=(a+c,b+d)\),

• \((a,b)(c,d):=(ac-bd,ad+bc)\).

Como vemos, la definición de suma es totalmente natural. Sin embargo, la de multiplicación no lo es. Más adelante entenderemos la utilidad de definirla de esta forma.

Para que nuestra extensión tenga validez, debemos comprobar que las operaciones que acabamos de definir, cuando se aplican sobre números reales, se reducen a las operaciones usuales en \(\mathbb{R}\). Veámoslo:

• \((a,0)+(c,0)=(a+c,0)\),

• \((a,0)+(c,0)=(ac-0,0+0)=(ac,0)\).

Hasta aquí parece que vamos bien. Pero ahora recordamos nuestro punto de partida. ¿La ecuación \(x^2+1=0\) tiene solución en \(\mathbb{C}\)? O, lo que es lo mismo, ¿existe algún número complejo, \(x\), tal que \(x^2=-1\)? Vamos a ver que el número complejo \((0,1)\) cumple esta propiedad:

\[ (0,1)^2=(0,1)(0,1)=(0-1,0+0)=(-1,0). \]

Como acabamos de comprobar, este número es especial. Lo designaremos con un nombre diferente. En general suele llamársele \(i\) en un contexto matemático y \(j\) en un contexto físico. Nosotros utilizaremos \(i=(0,1)\). Es sencillo conocer el resto de potencias de \(i\):

• \(i^2=-1\),

• \(i^3=i^2i=-i\),

• \(i^4=i^2i^2=(-1)(-1)=1\),

• \(i^5=i^4i=i\), y a partir de aquí se repiten. Por lo tanto para calcular \(i^n\) debemos dividir \(n\) entre \(4\) y el resto nos dará el valor que buscamos. Veamos un ejemplo:

\[ i^{325}=i^{4\cdot81+1}=\left(i^{4}\right)^{81}i^1=1\cdot i=i. \]

1.2.2. Forma binómica

Por la identificación de \(\mathbb{R}\) con el eje de abscisas de los complejos tenemos que el \((1,0)\) complejo es el \(1\) real. Podemos introducir ya otra forma de escribir los números complejos, que es conocida como forma binómica:

\[ (a,b)=a(1,0)+b(0,1)=a+ib. \]

Un número complejo, \(z\), puede escribirse entonces como \(z=a+ib\), siendo \(a\) su parte real y \(b\) su parte imaginaria.

Utilizando la multiplicación usual para los binomios podemos entender mejor la extraña definición de la multiplicación en \(\mathbb{C}\):

\[ (a+ib)(c+id)=ac+iad+ibc+i^2bd=(ac-bd)+i(ad+bc), \]

donde hemos utilizado que \(i^2=-1\).

1.2.3. Propiedades de la multiplicación

Vamos ahora a intentar profundizar en la multiplicación de los complejos.

• Elemento neutro. Lo que buscamos es un número complejo tal que cualquier otro multiplicado por éste permanezca inalterado. Como el elemento neutro en \(\mathbb{R}\) es el \(1\) parece lógico suponer que en \(\mathbb{C}\) sea el \((1,0)\). Veámoslo:

\[ (a,b)(1,0)=(a-0,b+0)=(a,b). \]

• Elemento inverso. Ahora, dado un complejo \(z=a+ib\in\mathbb{C}\), veremos que su inverso es

  \[ z^{-1}=\left(a+ib\right)^{-1}=\frac{a}{a^2+b^2}-i\frac{b}{a^2+b^2}. \]

  Para eso debemos verificar que al multiplicar estos dos números se obtiene el elemento neutro:

  \[ zz^{-1}=(a+ib)\left(\frac{a}{a^2+b^2}-i\frac{b}{a^2+b^2}\right)= \frac{a^2+b^2}{a^2+b^2}+i\frac{ab-ab}{a^2+b^2}=1. \]

• División.

\[ \frac{z_1}{z_2}=\frac{a+ib}{c+id}=(a+ib)\left(c+id\right)^{-1}=\left(a+ib\right) \left(\frac{c}{c^2+d^2}-i\frac{d}{c^2+d^2}\right). \]

Veremos dentro de un momento una forma más natural de definir la división en \(\mathbb{C}\). Antes de ello introducimos una noción que tiene especial interés.

Definición: Dado \(z=a+ib\in\mathbb{C}\) definimos su conjugado, \(\bar{z}\), como

\[ \bar{z}=a-ib. \]

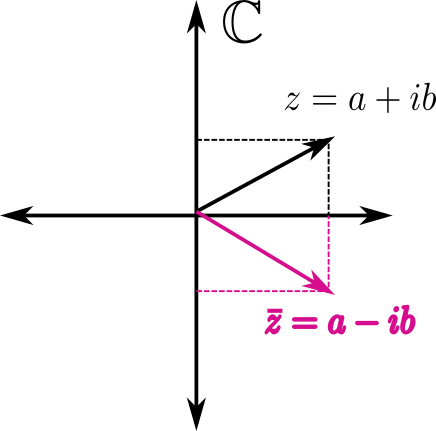
La principal ventaja de introducir el conjugado de un complejo es que al multiplicar un número por su conjugado el resultado es un número real,

\[ \left(a+bi\right)\cdot\left(a-bi\right)=a^2+b^2, \]

lo que nos permite simplificar algunas operaciones, como la división:

\[ \frac{5-2i}{7+3i}=\frac{\left(5-2i\right)\left(7-3i\right)}{\left(7+3i\right)\left(7-3i\right)} =\frac{29-29i}{7^2+3^2}=\frac{29}{58}\left(1-i\right). \]

1.2.4. Forma polar (o fórmula módulo/argumento)

Al mismo tiempo, el producto de un complejo por su conjugado también sirve para introducir una forma importante de representar los números complejos, la forma polar o forma módulo/argumento.

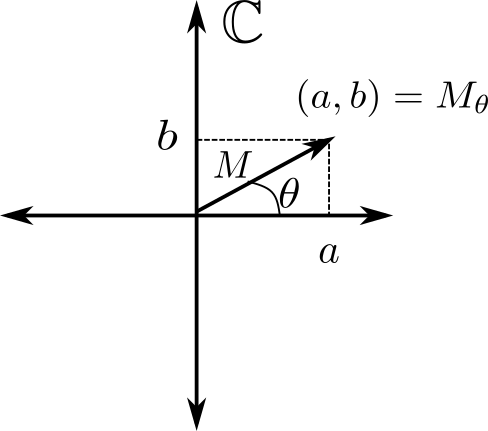
Esta forma de representar un número complejo se basa en el hecho de que un punto del plano queda perfectamente definido si conocemos sus componentes sobre los ejes \(OX\) y \(OY\) (representación cartesiana, \(z=(a,b)\)), pero también si conocemos la longitud del vector que une ese punto con el origen de coordenadas (módulo, \(M\)) y el ángulo que forma ese vector con el eje \(OX\) (argumento, \(\theta\)), como se muestra en la figura anterior. Ésta es la representación polar y suele escribirse \(z=M_{\theta}\). La manera de pasar de la representación cartesiana a la polar, y viceversa, se muestra en la siguiente tabla:

De cartesianas a polares	De polares a cartesianas
\(\displaystyle M=\sqrt{a^2+b^2}\)	\(a=M\cos\theta\)
\(\displaystyle \theta=\text{arctan}\left(\frac{b}{a}\right)\)	\(b=M\sin\theta\)

Destaquemos que del paso de la forma polar a la cartesiana (o, mejor dicho, a la binómica) resulta lo que se conoce como forma trigonométrica,

\[ M_{\theta}=M\cos\theta+iM\sin\theta=M\left(\cos\theta+i\sin\theta\right). \]

La forma polar permite simplificar la multiplicación y, por tanto, la división de complejos como sigue:

• Multiplicación:

  \[ \left(M_1\right)_{\theta_1}*\left(M_2\right)_{\theta_2}= \left(M_1*M_2\right)_{\theta_1+\theta_2}\]

• División:

  \[ \frac{\left(M_1\right)_{\theta_1}}{\left(M_2\right)_{\theta_2}} =\left(\frac{M_1}{M_2}\right)_{\theta_1-\theta_2}\]

Ahora es fácil introducir las potencias enteras de los números complejos. Observemos que

\[\begin{align*} \left(M_{\theta}\right)^2 &=& M_{\theta}*M_{\theta}=\left(M^2\right)_{2\theta}, \\ \left(M_{\theta}\right)^3 &=& \left(M^3\right)_{3\theta}, \end{align*}\]

y, siguiendo el razonamiento,

\[ \left(M_{\theta}\right)^n=\left(M^n\right)_{n\theta}. \]

Propiedad (Fórmula de De Moivre):

\[ \cos(n\theta)+i\sin(n\theta)=\left(\cos\theta+i\sin\theta\right)^n. \]

Demostración: Resulta de relacionar las potencias enteras con la representación trigonométrica de complejos, ya que, por un lado,

\[ \left(M_{\theta}\right)^n = \left(M^n\right)_{n\theta} = M^n\left(\cos(n\theta)+i\sin(n\theta)\right), \]

y, por otro,

\[ \left(M_{\theta}\right)^n =\left(M\left(\cos\theta+i\sin\theta\right)\right)^n = M^n\left(\cos\theta+i\sin\theta\right)^n. \]

Igualando estas dos expresiones obtenemos la igualdad de De Moivre.

1.2.5. Raíces enteras

Para concluir las operaciones elementales con números complejos nos falta el cálculo de raíces enteras en \(\mathbb{C}\). Éste es el punto esencial, lo que realmente justifica la introducción de \(\mathbb{C}\). ¡No debemos olvidar que el punto de partida era calcular la raíz cuadrada de \(-1\)!

Supongamos entonces que dado un número natural, \(n\in\mathbb{N}\), queremos calcular las raíces \(n-\)ésimas de un número complejo \(M_{\theta}\). Es decir, queremos encontrar los números complejos \(z=N_{\varphi}\in\mathbb{C}\) tales que

\[ \sqrt[n]{M_{\theta}}=z=N_{\varphi}, \]

o, lo que es lo mismo,

\[ M_{\theta}=z^n=\left(N_{\varphi}\right)^n=\left(N^n\right)_{n\varphi}=M_{\theta}. \]

Entonces, por un lado, tenemos que igualar los argumentos,

\[ N^n=M\Longrightarrow N=\sqrt[n]{M}, \]

es decir, \(N\) será la raíz \(n-\)ésima positiva del número real positivo \(M\) (que siempre existe). Por otro lado, tenemos que identificar los argumentos. Ahora debemos tener cuidado, porque una tentación es escribir que

\[ n\varphi=\theta\Longrightarrow \varphi=\frac{\theta}{n}, \]

pero no debemos olvidar que se trata de una identificación de ángulos y que si a un ángulo le sumamos un número entero de vueltas a la circunferencia (\(2\pi\), \(4\pi\),…) tendremos el mismo ángulo. Entonces se puede escribir

\[ n\varphi=\theta+2k\pi \Longrightarrow \varphi=\frac{\theta+2k\pi}{n}, \qquad k=0,1,...,n-1. \]

¿Por qué paramos en \(k=n-1\)? Porque para \(k=n\) obtendríamos \(\frac{\theta+2n\pi}{n}=\frac{\theta}{n}+2\pi=\frac{\theta}{n}\), es decir, el mismo ángulo que para \(k=0\).

Resumiendo, todo número complejo, \(M_{\theta}\), tiene \(n\) raíces complejas,

\[\begin{split} \sqrt[n]{M_{\theta}}=N_{\varphi},\qquad\mbox{con } \left\{\begin{array}{l} N=\sqrt[n]{M},\\ \\ \varphi=\frac{\theta+2k\pi}{n},\quad k=0,1,...,n-1. \end{array}\right. \end{split}\]

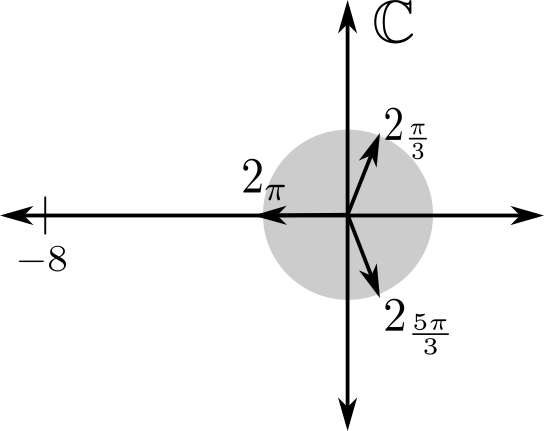
Por ejemplo, vamos a calcular las raíces cúbicas de \(-8\), que, como número complejo, se puede escribir \(8_{\pi}\).

\[\begin{split} \sqrt[3]{-8}=\sqrt[3]{8_{\pi}}= \left\{\begin{array}{l} \left(\sqrt[3]{8}\right)_{\frac{\pi+0}{3}}=\left(2\right)_{\frac{\pi}{3}},\\ \left(\sqrt[3]{8}\right)_{\frac{\pi+2\pi}{3}}=\left(2\right)_{\pi},\\ \left(\sqrt[3]{8}\right)_{\frac{\pi+4\pi}{3}}=\left(2\right)_{\frac{5\pi}{3}}.\\ \end{array}\right. \end{split}\]

A continuación mostramos la representación gráfica de estas raíces cúbicas:

Ejercicios:

1. Calcula: \(\displaystyle\frac{(3-2i)(2+3i)}{3-4i}\), \(\displaystyle\frac{(1-i)(2+i)}{5+3i}\), \(\displaystyle i^{5787}\).

2. Expresa en forma polar los números complejos \(z_1=1+i\) y \(z_2=(2,-2)\).

3. Expresa en forma binómica los números complejos \(z_3=2_{\frac{\pi}{2}}\) y \(\sqrt{2}_{\frac{3\pi}{4}}\).

4. Calcula: \((1+4i)^3\), \((1+i)^4\), \((2-2i)^5\), \(\displaystyle\sqrt[4]{1}\), \(\displaystyle\sqrt[5]{243\left(\frac{\sqrt{3}}{2}+\frac{1}{2}i\right)}\).

5. Puedes seguir practicando en la página web del grupo de innovación educativa GieMATic, de la Universidad de Cantabria: https://www.giematic.unican.es/index.php/numeros-complejos/material-interactivo