Boletín 1: Funciones reales de una variable real
2.8. Boletín 1: Funciones reales de una variable real#
Te dejamos aquí algunos ejercicios para que practiques lo que has dibido aprender en este capítulo. ¡Ánimo!
Ordena los números siguientes de menor a mayor. Indica a cuál de los conjuntos siguientes: naturales, enteros, racionales o irracionales, pertenecen dichos números. Nota: Indica sólo el conjunto más pequeño al que pertenece cada número; por ejemplo \(2\in \mathbb{N}\) y \(0.5\in \mathbb{Q}\).
Número
\(0.25\)
\(\sqrt{2}\)
\(\dfrac{15}2\)
\(0.102024\)
\(-\sqrt{4}\)
\(\dfrac{12}4\)
\(2.333\dots\)
\(3\)
Conjunto
\(\vphantom{\dfrac{2}{3}}\)
Calcula o simplifica cuando sea posible:
\[\begin{split} \begin{array}{llll} \text{(a)} \ln (\mathbf{e}) & \text{(b)} \ln (\mathbf{e}^2) & \text{(c)} \ln (0) & \text{(d)} \ln (-1) \\ \text{(e)} \ln(2) & \text{(f)} \mathbf{e}^0 & \text{(g)} \mathbf{e}^{-1} & \text{(h)} \mathbf{e}^{\ln (1)} \\ \text{(i)} \mathbf{e}^{\ln (\mathbf{e})} & \text{(j)} \mathbf{e}^{\ln(\mathbf{e}^3)} & \text{(k)} \ln \sqrt{2^3} & \text{(l)} \dfrac{\ln (5x)}{\ln \left( \frac{5}{x} \right)} \\ \text{(m)} \dfrac{\ln (5+x)}{\ln (5-x)} \qquad & \text{(n)} \ln (\mathbf{e}^2) \mathbf{e}^{\ln (5+x) - \ln (5x)} \qquad & \text{(ñ)} \ln \left( \dfrac{x^2-1}{x^3} \right)^3 \qquad & \end{array} \end{split}\]Resuelve las ecuaciones siguientes:
\[\begin{split} \begin{array}{ll} \text{(a)} \sqrt{x-3}+5=x & \text{(b)} \mathbf{e}^{x-3}=30 \\ \text{(c)} 9^{2x+1}=27 & \text{(d)} 10^{5x}=1000 \\ \text{(e)} \mathbf{e}^{x^2-1}=9 & \text{(f)} \ln(x-3)=5 \\ \text{(g)} \ln(x+2)+\ln(x-2)=1 \qquad & \text{(h)} \log_3(x^2)-\log_3(2x)=2 \end{array} \end{split}\]¿Dónde está el error en el razonamiento siguiente?
\(\sqrt{25}=\sqrt{5^2}=5\quad\) implica que \(\quad\sqrt{25}=\sqrt{(-5)^2}=-5.\quad\) Entonces: \(\quad 5 = -5\)
Si \(a>0\) entonces:
\(|x| = a\) significa que \( x=\dots \) o bien \(x = \dots \)
\(|x| < a\) significa que \(\dots\)
\(|x| \geq a\) significa que \(\dots\)
Resuelve las ecuaciones siguientes:
a. \(|2x-4|=6\)
b. \(|7x-3|=-2\)
c. \(|2x+4|=|5x-2|\)
Resuelve las inecuaciones siguientes:
a. \(|3x-2|\le10\)
b. \(|6x+1|<2\)
c. \(|-4x+3|>1\)
d. \(|5x-1|\ge 2\)
Completa la siguiente tabla con los valores correspondientes:
Ángulo
\(0\)
\(\dfrac{\pi}{6}\)
\(\dfrac{\pi}{4}\)
\(\dfrac{\pi}{3}\)
\(\dfrac{\pi}{2}\)
\(\pi\)
\(\dfrac{3\pi}{2}\)
\(2\pi\)
Seno
Coseno
Tangente
Cotangente
Secante
Cosecante
Determina el ángulo \(\alpha\in[0,2\pi)\) tal que
a. \(\sin(\alpha)=-\dfrac{\sqrt{3}}{2}\)
b. \(\tan(\alpha)=\sqrt{3}\)
Ecuación de la recta:
a. Calcula la ecuación de la recta que pasa por el punto \((2,-1)\) y tiene pendiente \(3\).
b. Calcula la ecuación de la recta que pasa por los puntos \((1,-1)\) y \((2,3)\).
c. Sin calcular la ecuación, responde a la siguiente pregunta: ¿puede una recta pasar por los puntos \((0,2)\), \((2,1)\) y \((4,-1)\)?
d. Escribe la ecuación de una recta paralela a la recta \(y=x\).
e. Escribe la ecuación de la recta paralela a la recta \(y=x\) que pasa por el punto \(P=(2, -1)\).
f. Escribe la ecuación de la recta horizontal que pasa por el punto \((3,\frac{7}{2})\).
g. Escribe la ecuación de la recta vertical que pasa por el punto \((-1,\frac{5}{3})\).
h. Calcula la ecuación de la recta que pasa por el punto \((1,4)\) y es perpendicular a la recta de ecuación \(2y-5x+7=0\).
i. Calcula la ecuación de la recta que pasa por \((-1,-1)\) y es paralela a la que pasa por los puntos \((0,1)\) y \((5,0)\).
j. Si la capacidad pulmonar cae del \(100\%\) a los 20 años hasta el \(40\%\) a la edad de 80 años, y se supone una relación lineal, obtén esa relación lineal y calcula la edad a la que corresponde un \(25\%\) de capacidad pulmonar.
Calcula la ecuación de las circunferencias:
a. de centro \((0,0)\) y radio \(2\);
b. de centro \((1,2)\) y radio \(3\);
c. de centro \((-1,2)\) y radio \(4\).
Calcula la ecuación de la parábola que pasa por los puntos \((-2,13)\), \((2,1)\) y \((4,1)\).
Determina el dominio máximo de la siguiente función:
\[ f(x)=\frac{3x - \tan(2x)}{\sqrt{1-x^2}}. \]El coste \(C\) de enviar un paquete por una empresa de transporte depende del peso \(p\) en gramos, como sigue:
\[\begin{split} C(p) = \left\{\begin{array}{cl} 0.8 \, & \quad \text{si } p \in [0,10), \\ 1 + 0.2\,p \, & \quad \text{si } p \in [10,20), \\ 1 + 0.1\,p \, & \quad \text{si } p \in [20,30), \\ p^2 \, & \quad \text{si } p \in [30,\infty). \\ \end{array}\right. \end{split}\]Dibuja la gráfica de la función \(C\), indicando su dominio y su rango, y estudia el crecimiento de la función.
Analiza si cada una de las funciones siguientes es par, impar o ninguna de las dos cosas:
a. \(f_1(x)=3x-x^2\)
b. \(f_2(x)= 2x^3-x\)
c. \(f_3(x)=\displaystyle\frac12x^4+e^{x^2}+5\)
d. \(f_4(x)=\displaystyle\frac{\tan(x)+\sin(x)}{\cos(x^{2})}\)
e. \(f_6(x)=\displaystyle\frac{x^{4}\sin^{3}(x)}{\tan(x)} \)
f. \(f_7(x)=\left\vert x\right\vert (x+1)^{2}\)
g. \(f_8(x)=\displaystyle\frac{x^{4}-\cos(x)}{x^{2}-\sin(x)}\)
¿Qué propiedad gráfica caracteriza a una función par? ¿Y a una impar?
Analiza si cada una de las funciones siguientes es periódica. En caso afirmativo, determina su periodo.
a. \(f_1(x)=\sin(3x)\)
b. \(f_2(x)= \cos(x-2)\)
c. \(f_3(x)=\cos(x)-2\)
d. \(f_4(x)=\displaystyle\tan(x-\frac{\pi}{2})\)
e. \(f_5(x)=\displaystyle 4\sin(x) + 3\cos(2x) - 5 \sin(\frac{2}{5}x)\)
Sean \(f(x)=\displaystyle\frac{6x}{x^{2}-9}\) y \(g(x)=\sqrt{3x}\).
Primero calcula \((f\circ g)(12)\), luego \((f\circ g)(x)\) y, por último, encuentra el dominio de \(f\circ g\).
Elige la opción correcta. Dadas \( f(x)=\displaystyle{\frac{4x^2+1}{x-1}}\) y \( g(x)=\displaystyle{\frac{x-1}{x^2}}\), entonces
a. \((f\circ g)(1)=-1\,\) y \(\,(g\circ f)(1)=0\)
b. \((f\circ g)(2)=-5/3\,\) y \(\,(g\circ f)(0)=-2\)
c. \((f\circ g)(-1)=17/3\,\) y \(\,(g\circ f)(-1)=g(5/2)\)
d. ninguna de las otras respuestas es correcta
El agua de un charco de forma circular se evapora lentamente por el efecto del sol. Después de \(t\) minutos el radio del charco mide \(18/(2t+3)\,\)cm. Expresa el área \(A\) del charco en función del tiempo. Relaciona lo que has hecho con el concepto de composición de funciones.
Se sabe que el número \(n\) de ordenadores de sobremesa de los laboratorios de una facultad de Informática se incrementa cada curso académico, en función del número \(x\) de alumnos admitidos en la facultad, según la fórmula
\[n(x) = 10+0.05x.\]También se sabe que el número \(x\) de alumnos admitidos en cada curso académico depende del número \(a\) de alumnos de bachillerato científico-tecnológico que han aprobado las pruebas ABAU, según la fórmula
\[x(a)=100+\sqrt{\frac{a}{12}}.\]a. Expresa el número de ordenadores en función del número de aprobados en las pruebas ABAU.
b. Estima el número de ordenadores que tendría que comprar la facultad el próximo curso si aprobasen las pruebas EBAU 4800 alumnos de bachillerato científico-tecnológico.
c. Halla la fórmula que calcula el número de aprobados conociendo el número de admitidos en la facultad.
¿Existe la inversa de la función de la figura? ¿Por qué?
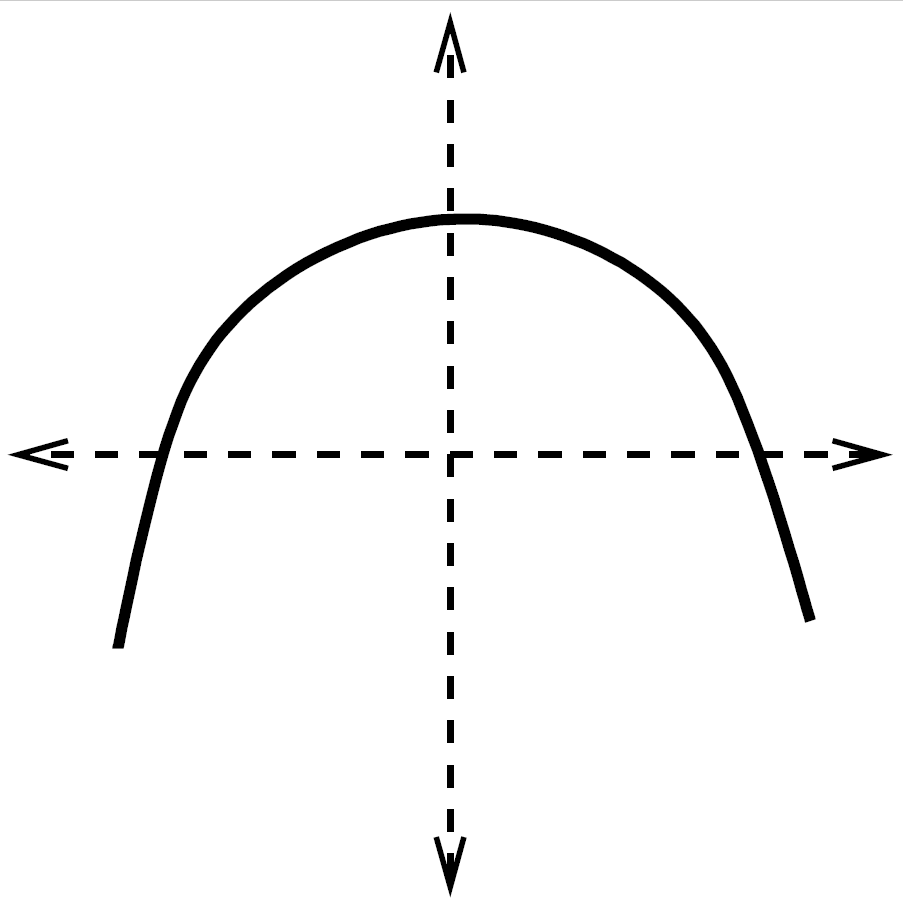
Comprueba que las funciones siguientes son inversas entre sí:
\[ f(u)=\frac{u-1}{u+1}\,, \qquad g(u)=\frac{u+1}{1-u}\,. \]Elige la opción correcta. La función inversa de \(f\) dada por \(f(x)=e^{x^3+1}\) es:
a. \(f\) no tiene función inversa
b. \(\ln{(x^3+1)}\)
c. \(\sqrt[3]{\ln(y)-1}\)
d. \(\displaystyle{\frac{1}{e^{x^3+1}}}\)
Calcula, en caso de existir, la inversa de las siguientes funciones:
a. \(f_1(x) = x^3+5\)
b. \(f_2(x) =\sin(2x-7)\)
c. \(f_3(x) = \textbf{e}^{2x}\)
d. \(f_4(x)=\displaystyle\frac{1}{5}+e^{x}\)
e. \(f_5(x)=\sqrt{2x-3}\)
f. \(f_6(x)=\sqrt[3]{\frac{x+1}{2}}\)
g. \(f_7(x)=\displaystyle\frac{1+x^{2}}{x^{2}}\)
¿Cuál o cuáles de las siguientes funciones son polinomios?
a. \(f_1(x) = x^2+6x^{-3}\)
b. \(f_2(x) = x^{\frac{2}{3}}-6x^3\)
c. \(f_3(x) = \dfrac{x^4+6x^3}{x^2+6x-7}\)
d. \(f_4(x) = x^4+6x^3\)
Un panadero desea mezclar harina de centeno, a 10 euros el kilo, con harina de trigo, a 24 euros el kilo, con el fin de obtener 100 kilos de harina de mezcla que venderá a 18 euros el kilo. ¿Cuántos kilos de harina de centeno y cuántos de harina de trigo debe mezclar?
Se conoce como ventana normanda a aquella en forma de rectángulo rematado por un semicírculo. Si el perímetro de una ventana normanda es \(5.5\) metros, expresa el área de la ventana como función del ancho \(x\) de la misma.
Responde a las siguientes cuestiones:
a. Halla un número racional y otro irracional situados entre \(3^{500}\) y \(3^{500}+1\).
b. Encuentra un número real \(\alpha\) tal que \(\alpha^{2}\) sea irracional y \(\alpha^{4}\) sea racional.
c. Encuentra dos números irracionales tales que su suma y su producto sean racionales.
d. Dada \(f(x)=2^x-3,\) ¿cuál es el dominio de \(f^{-1}\)?

