2.5. Continuidad

2.5.1. Continuidad en un punto

Definition

Sea \(f:A\subset\mathbb{R}\rightarrow\mathbb{R}\), \(x_0\in A\). Diremos que \(f\) es continua en \(x_0\) si y sólo si existe \(\displaystyle\lim_{x\to x_0} f(x)\) y ese límite es \(f(x_0)\).

Es decir, \(f\) es continua en \(x_0\) si y sólo si

\[ \forall\epsilon>0, \exists\delta>0 \Big/ \left|x-x_0\right|<\delta\Rightarrow\left|f(x)-f(x_0)\right|<\epsilon. \]

Observemos que, respecto a la definición de límite hay una pequeña diferencia. Antes escribíamos

\[ 0< \left|x-x_0\right|<\delta, \]

mientras que en el caso de la continuidad escribimos simplemente

\[ \left|x-x_0\right|<\delta. \]

¿Por qué? Cuando hablamos de límite nos interesa que el punto \(x_0\) no intervenga en la definición, para poder tener límites de funciones que ni siquiera estén definidas en \(x_0\). De ahí ese \(0<|x-x_0|\) (evidentemente, \(0=|x-x_0|\) si y sólo si \(x=x_0\)). Sin embargo, en el caso de la continuidad, incluir el punto \(x_0\) es natural. Además, en la continuidad, no puede estropear nada, porque si \(x=x_0\) se tiene que \(|f(x)-f(x_0)|\) es \(0\), por lo que será siempre menor que cualquier \(\epsilon\) positivo.

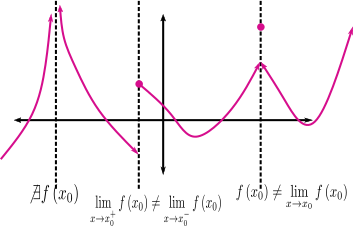
En la siguiente figura mostramos gráficamente los posibles casos en los que falla la continuidad. A los dos primeros (\(\not\exists f(x_0)\), \(\displaystyle\not\exists\lim_{x\to x_0}f(x)\)) se les llama discontinuidades esenciales, mientras que el tercer caso (\(\displaystyle \lim_{x\to x_0}f(x)\not=f(x_0)\)) es una discontinuidad evitable.

Algunas propiedades importantes de la continuidad son las siguientes.

Property (Álgebra de las funciones continuas)

Sean \(f,g:A\subset\mathbb{R}\rightarrow\mathbb{R}\) funciones continuas en un punto \(x_0\in A\). Entonces

• \(\lambda f\) es continua en \(x_0\), \(\forall\lambda\in\mathbb{R}\),

• \(f\pm g\) es continua en \(x_0\),

• \(fg\) es continua en \(x_0\),

• si \(g(x_0)\not=0\), \(\frac{f}{g}\) es continua en \(x_0\).

Property

La composición de funciones continuas es una función continua. Es decir,

\[\begin{split} \left.\begin{array}{l} f:A\subset\mathbb{R}\rightarrow\mathbb{R} \text{ continua en } x_0\in A \\ g:f(A)\rightarrow\mathbb{R}\text{ continua en }f(x_0) \end{array}\right\}\Longrightarrow g\circ f:A\subset\mathbb{R}\rightarrow\mathbb{R} \text{ continua en }x_0\in A. \end{split}\]

Property

El límite conmuta con las funciones continuas. Es decir, sean \(f\) y \(g\) funciones tales que existe \(\displaystyle\lim_{x\to x_0}f(x)=l\in\mathbb{R}\) y \(g\) es una función continua en \(l\). Entonces

\[ \lim_{x\to x_0}g\left(f(x)\right)=g\left(\lim_{x\to x_0}f(x)\right)=g(l). \]

Así, por ejemplo,

\[ \lim_{x\to 1}\sin\left(\frac{\ln x+\cos^2 x}{e^x+2x}\right)=\sin\left(\lim_{x\to 1}\frac{\ln x+\cos^2 x}{e^x+2x}\right), \]

ya que la función ``seno’’ es continua.

Remark

Si sientes curiosidad, anímate y mira el artículo de Luisa Cuadrado y Rafael Crespo, para la Real Sociedad de Matemáticas Española, titulado Sin levantar el lápiz del papel sobre el concepto de continuidad. ¡Muy divertidas las ilustraciones con las tuberías de Mario! https://drive.google.com/file/d/1YaWLuzdmRXvRRGpG8GmUffZqKZrnbt6s/view.

2.5.2. Continuidad en intervalos

Ahora que ya tenemos bien definida la continuidad puntual, vamos a definir la continuidad en intervalos, tanto abiertos como cerrados.

Definition

1. Sea \(f:(a,b)\subset\mathbb{R}\rightarrow\mathbb{R}\). Diremos que \(f\) es continua en \((a,b)\) si es continua en todos los puntos de \((a,b)\).

2. Sea \(f:[a,b]\subset\mathbb{R}\rightarrow\mathbb{R}\). Diremos que \(f\) es continua en \([a,b]\) si

   a. \(f\) es continua en \((a,b)\),

   b. \(f\) es continua en \(a\) por la derecha,

   c. \(f\) es continua en \(b\) por la izquierda.

Definition

Sea \(f:A\subset\mathbb{R}\rightarrow\mathbb{R}\). Diremos que \(x_0\in A\) es una raíz de \(f\) si \(f(x_0)=0\).

2.5.3. Teoremas de Bolzano y Weierstrass

Theorem (Teorema de Bolzano)

Sea \(f:[a,b]\rightarrow\mathbb{R}\) una función continua en \([a,b]\) tal que \(f(a)f(b)<0\). Entonces existe \(x_0\in(a,b)\) tal que \(f(x_0)=0\).

El teorema de Bolzano habla de la existencia de raíces para funciones continuas. Debemos hacer algún comentario sobre él:

1. Pueden existir varias raíces, como se muestra en el gráfico de la derecha en la figura anterior.

2. Si se suprime alguna de las hipótesis, el teorema, en general, no es válido, como se muestra en la siguiente figura.

Theorem (Teorema de Weierstrass)

Sea \(f:[a,b]\rightarrow\mathbb{R}\) una función continua en \([a,b]\). Entonces \(f\) alcanza máximo y mínimo absoluto en \([a,b]\). Es decir,

\[ \exists x_1, x_2\in[a,b]\Big/ f(x_1)\leq f(x)\leq f(x_2)\qquad\forall x\in[a,b]. \]