3.4. Aplicaciones de la derivada#

3.4.1. Extremos relativos y absolutos#

Supongamos un intervalo abierto \(A \subset \mathbb{R}\) y una aplicación \(f : A \longrightarrow \mathbb{R}\).

Definition

Decimos que \(f\) presenta un máximo relativo en \(a \in A\) si y sólo si existe \(h > 0\) tal que

\[\begin{equation*} f(x) \leq f(a) , \quad \forall x \in (a-h,a+h) \, . \end{equation*}\]

Análogamente, decimos que \(f\) presenta un mínimo relativo en \(a \in A\) si y sólo si existe \(h > 0\) tal que:

\[\begin{equation*} f(x) \geq f(a) , \quad \forall x \in (a-h,a+h) \, . \end{equation*}\]

Por extremo relativo entendemos, indistintamente, un máximo o un mínimo relativo.

Definiremos, a continuación, punto crítico (o punto estacionario) y, acto seguido, nos ponemos a estudiar la relación entre extremos relativos y puntos críticos.

Definition

Si en un punto \(a\) se tiene \(f'(a) = 0\), decimos que \(a\) es un punto crítico (o estacionario) de la función \(f\).

En cuanto a la relación entre puntos críticos y extremos relativos (que tienden a confundirse… aunque no son lo mismo), en primer lugar, tenemos que destacar que un extremo relativo puede ser un punto en el que ni siquiera exista derivada (y, por lo tanto, no será punto crítico). El ejemplo más clásico es la función valor absoluto. Si recuerdas su dibujo, verás fácilmente que esta función tiene un mínimo relativo en \(x=0\)… ¡pero en ese punto la función valor absoluto no es derivable!

Para cubrir esta primera posibilidad vamos a ver el primer criterio para localizar extremos relativos. Suele conocerse por criterio de la primera derivada y, si lo lees atentamente, verás que pedimos que la función sea derivable cerca del punto en cuestión, pero no necesariamente en él (es decir, valdría para la función valor absoluto en \(x_{0}=0\)):

Property (Criterio de la primera derivada)

Sea \(f:[a,b] \longrightarrow \mathbb{R}\) una función continua, \(x_0 \in (a,b)\) y sea \(r > 0\) tal que \(f\) es derivable en \((x_0-r,x_0) \cup (x_0,x_0+r)\). Entonces

  • Si \(f'(x)<0\), \(\forall x\in (x_0-r,x_0)\) y \(f'(x)>0\), \(\forall x\in (x_0,x_0+r)\), entonces \(f\) presenta en \(x_0\) un mínimo relativo.

  • Si \(f'(x)>0\), \(\forall x\in (x_0-r,x_0)\) y \(f'(x)<0\), \(\forall x\in (x_0,x_0+r)\), entonces \(f\) presenta en \(x_0\) un máximo relativo.

Pero, ¿qué pasa si la función sí es derivable en un extremo relativo? En este caso, tenemos el siguiente teorema:

Theorem

Si \(f\) presenta un extremo relativo en el punto \(a \in A\) y \(f\) es derivable en dicho punto, entonces \(f'(a) = 0\).

Fíjate bien en que la condición anterior es necesaria, pero no suficiente: la función puede presentar derivada nula en un punto, pero no tener un extremo en él. Es decir, para funciones derivables, extremo relativo \(\Rightarrow\) punto crítico, pero punto crítico \(\not\Rightarrow\) extremo relativo.

Por ejemplo, la función \(f(x) = x^3\) verifica \(f'(0) = 0\), pero no se trata de un máximo ni de un mínimo.

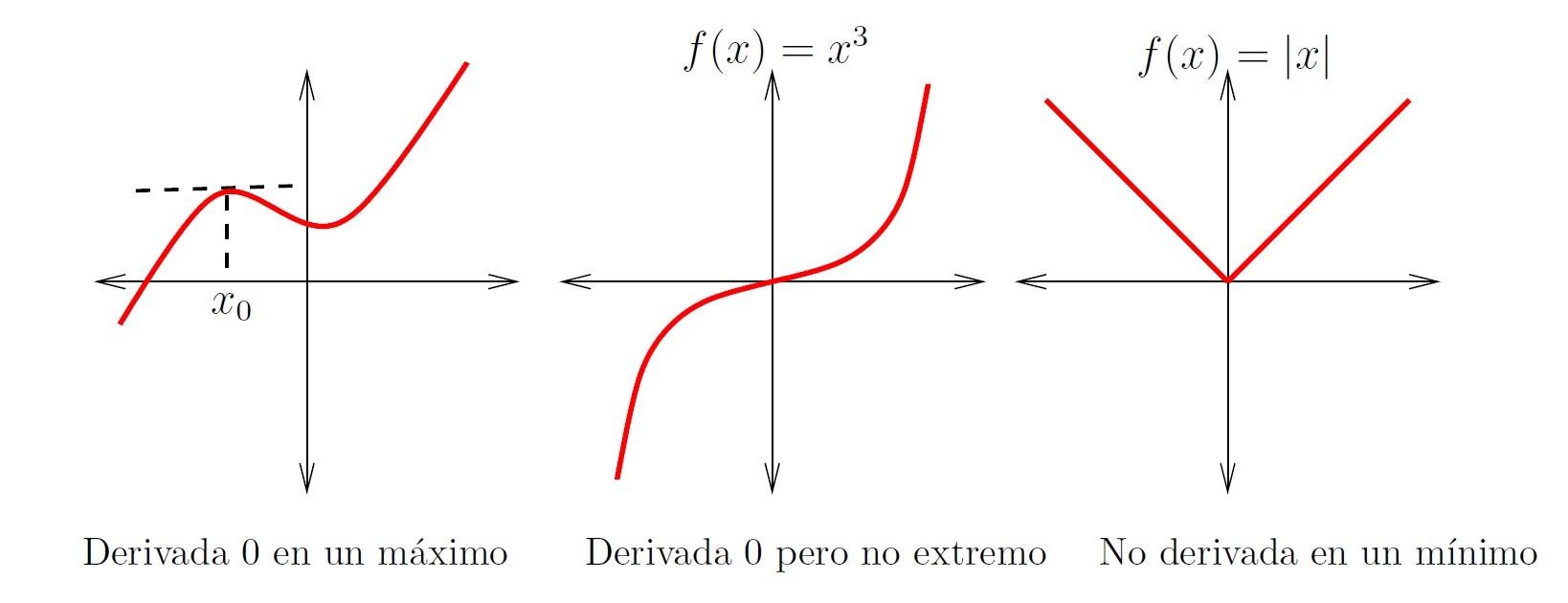
Intentamos ilustrar esta extraña relación en la siguiente figura: ../../_images/cap_deriv_ext_criticos.jpg

Entonces, resumiendo lo que acabamos de ver, cuando nos interesa localizar los extremos relativos de una función en un determinado intervalo (abierto), lo primero que haremos será buscar sus puntos críticos (es decir, buscar los \(x\) tales que \(f'(x)=0\)) y, a continuación, aplicar alguno de los criterios para la identificación de extremos relativos. Ya hemos visto el de la primera derivada, vamos a ver ahora el más utilizado:

Property (Criterio de la segunda derivada)

Sea \(f: (a,b) \longrightarrow \mathbb{R}\) con derivada segunda continua en \((a,b)\). Sea \(x_0 \in (a,b)\) tal que \(f'(x_0) = 0\). Entonces:

  • si \(f''(x_0) < 0\), \(f\) presenta en \(x_0\) un máximo relativo,

  • si \(f''(x_0) > 0\), \(f\) presenta en \(x_0\) un mínimo relativo.

¿Y si no podemos aplicar la propiedad anterior? Es decir, si hemos encontrado un punto \(x_{0}\) en el que \(f'(x_{0})=0\) y \(f''(x_{0})=0\), ¿qué hacemos? Pues utilizar el siguiente criterio:

Property (Criterio de la n-ésima derivada)

Sea \(f \in \mathcal{C}^{n} (a,b)\) para algún \(n \geq 1\). Sea \(x_0 \in (a,b)\) tal que \(f'(x_0) = f''(x_0) = \ldots = f^{(n-1)}(x_0) = 0\) y \(f^{(n)}(x_0) \neq 0\). Entonces

  • Si \(n\) es par y \(f^{(n)}(x_0)<0\), \(f\) presenta en \(x_0\) un máximo relativo.

  • Si \(n\) es par y \(f^{(n)}(x_0)>0\), \(f\) presenta en \(x_0\) un mínimo relativo.

  • Si \(n\) es impar, \(f\) no tiene extremo relativo en \(x_0\).

Definition

Se denomina supremo e ínfimo de \(f\) en \(A\), respectivamente, a las cantidades:

\[\begin{equation*} \underset{x \in A}{\sup} f(x) \quad \quad \text{ e } \quad \quad \underset{x \in A}{\inf} f(x) \, , \end{equation*}\]

es decir, al supremo e ínfimo del conjunto imagen \(f(A)\).

Cuando el supremo o el ínfimo de \(f\) en \(A\) existen y pertenecen a \(f(A)\), se denominan máximo absoluto y mínimo absoluto de \(f\) en \(A\), respectivamente.

El máximo y el mínimo absoluto se denominan, globalmente, extremos absolutos.

Entonces, para encontrar los extremos (máximos y mínimos) absolutos de una función en un intervalo cerrado \([a,b]\), debemos estudiar:

  • los puntos estacionarios de \(f\) en \((a,b)\), es decir, los puntos \(x\in (a,b)\) tales que \(f\) es derivable y \(f'(x) = 0\),

  • los puntos donde \(f\) no es derivable,

  • los extremos (\(a\) y \(b\)) del intervalo.

En la siguiente figura, mostramos un ejemplo de una función continua en un intervalo cerrado y acotado, para la que el mínimo absoluto se encuentra en los dos puntos en los que la función es no derivable (mismo valor en ambos puntos), mientras que el máximo absoluto está en el extremos de la derecha del intervalo (aunque podría haber estado en el punto crítico que vemos para \(x=\frac{\pi}{2}\)).

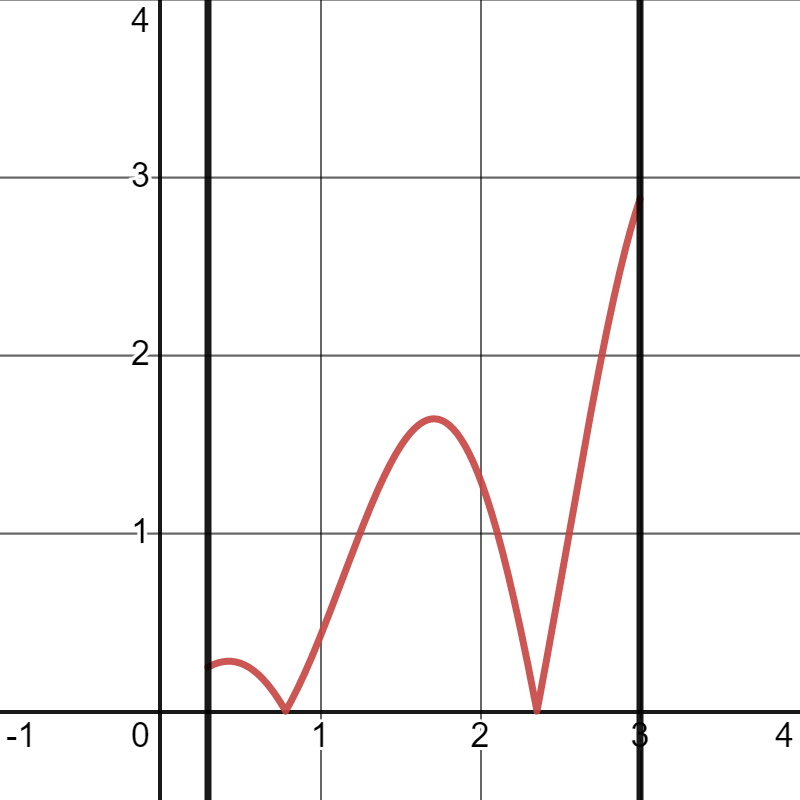
../../_images/cap_deriv_extremos_absolutos.png

Ya conocéis, de bachillerato, los problemas en los que hay que buscar el máximo y el mínimo absoluto de una función (continua) en determinado intervalo cerrado y acotado. Suelen disfrazarse con un texto más o menos imaginativo (Cortamos una hoja cuadrada de cartón de forma que […]). Aquí tenéis 10 ejemplos (de diferentes tipos), para que vayáis practicando: https://existelimite.blogspot.com/search/label/Máximos y mínimos.

3.4.2. Teoremas de Rolle y Lagrange#

Theorem (Teorema de Rolle)

Sea una aplicación \(f : [a,b] \longrightarrow \mathbb{R}\), continua en \([a,b]\) y derivable en \((a,b)\). Si \(f(a) = f(b)\), entonces existe un punto \(\xi \in (a,b)\) tal que:

\[\begin{equation*} f^{\prime} (\xi) = 0 \, . \end{equation*}\]
images/cap_deriv_Rolle.png

Debemos hacer algún comentario sobre este teorema.

Remark

  1. El teorema nos dice que existe una raíz de \(f'\). Puede existir más de una. No hablamos de unicidad.

  2. Si \(f\) cumple las hipótesis del teorema y tiene \(n\) raíces reales, \(f'\) tendrá, al menos, \(n-1\) raíces reales.

    Este hecho se ilustra en la siguiente figura. Según el teorema de Rolle, entre dos raíces de \(f\) (es decir, dos puntos donde \(f\) vale \(0\)) tiene que haber, por lo menos, una raíz de \(f'\).

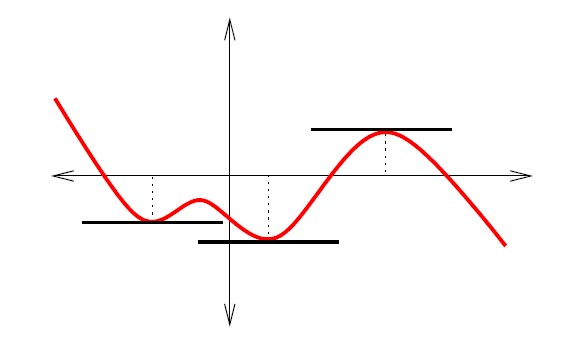
    ../../_images/cap_deriv_remark_Rolle.jpg

  3. Recíprocamente, si \(f'\) tiene \(n\) raíces reales, \(f\) tendrá, a lo sumo, \(n+1\) raíces reales.

A continuación vamos a ver un ejercicio en el que se muestra una aplicación típica del teorema de Rolle: mostrar la unicidad de una raíz.

Example

Demostrar que la ecuación

\[ x+\sin x=\frac{1}{\sqrt{x}+3} \]

tiene exactamente una raíz en \([0,\pi]\).

Solución:

En primer lugar, vamos a re-escribir nuestro problema como el cálculo de las raíces de una función. Sólo hay que darse cuenta de que la ecuación que nos dan se puede escribir

\[ x+\sin x-\frac{1}{\sqrt{x}+3}=0, \]

y, por tanto, es lo mismo que buscar las raíces de la función

\[ f(x)=x+\sin x-\frac{1}{\sqrt{x}+3}. \]

Vamos a demostrar que esta función tiene raíz en \([0,\pi]\) (utilizando el teorema de Bolzano), y, a continuación, que esta raíz es única, con el teorema de Rolle.

Existencia

\[\begin{split} \left.\begin{array}{l} f\mbox{ continua en }[0,\pi] \\ f(0)=0+\sin 0-\frac{1}{\sqrt{0}+3}=-\frac{1}{3}<0 \\ f(\pi)= \pi+\sin \pi-\frac{1}{\sqrt{\pi}+3}=\pi-\frac{1}{\sqrt{\pi}+3}>0 \end{array}\right\} \stackrel{\mbox{(Bolzano)}}{\Longrightarrow} \mbox{Existe raíz de $f$ en }[0,\pi]. \end{split}\]

Unicidad

Para probar la unicidad razonaremos por reducción al absurdo. Según el teorema de Rolle, si \(f\) tuviera dos raíces en \([0,\pi]\), habría algún punto entre ellas (por lo tanto en \((0,\pi)\)) en el que \(f'\) se anularía. Veamos que esto no es posible. Derivando,

\[ f'(x)=1+\cos x+\frac{1}{2\sqrt{x}\left(\sqrt{x}+3\right)^2}. \]

Como

\[\begin{split} \left.\begin{array}{ll} 1+\cos x>0&\quad\forall x\in(0,\pi) \\ \dfrac{1}{2\sqrt{x}\left(\sqrt{x}+3\right)^2}>0&\quad\forall x\in(0,\pi) \end{array}\right\} \Rightarrow f'(x)=1+\cos x+\frac{1}{2\sqrt{x}\left(\sqrt{x}+3\right)^2}>0\quad\forall x\in(0,\pi), \end{split}\]

lo que contradice el que exista un punto en el que \(f'\) se anula. Por lo tanto, es imposible que haya dos raíces distintas de \(f\) en \([0,\pi]\).

Theorem (Teorema del valor medio de Lagrange)

Sea una aplicaci’{o}n \(f : [a,b] \longrightarrow \mathbb{R}\) continua en \([a,b]\) y derivable en \((a,b)\). Entonces, existe un punto \(\xi \in (a,b)\) tal que:

\[\begin{equation*} f(b) - f(a) = f' (\xi) (b - a) \, . \end{equation*}\]
images/cap_deriv_Lagrange.png

Basta recordar que \(\displaystyle\frac{f(b) - f(a)}{b-a}\) es la pendiente de la recta secante a \(f\) por \(a\) y \(b\) para tener la interpretación geométrica de este teorema, que mostramos en la imagen anterior: existe un punto \(x_0\in(a,b)\) de forma que la recta tangente a \(f\) por ese punto es paralela a dicha recta secante.

como una consecuencia inmediata del teorema anterior, tenemos la siguiente propiedad:

Property

Sea \(f\) una función real derivable en \((a,b)\).

  • Si \(f' (x) \geq 0\), \(\forall x \in (a,b)\), entonces \(f\) es monótona creciente.

  • Si \(f' (x) \leq 0\), \(\forall x \in (a,b)\), entonces \(f\) es monótona decreciente.

  • Si \(f' (x) = 0\), \(\forall x \in (a,b)\), entonces \(f\) es constante.

  • Si \(f' (x) \neq 0\), \(\forall x \in (a,b)\), entonces \(f\) es inyectiva.

La deducción de este resultado es sencilla. Pensemos, por ejemplo, en el primer punto de la propiedad. Si \(f' (x) \geq 0\), \(\forall x \in (a,b)\), aplicando el resultado del Teorema de Lagrange, resulta que \(f(b)-f(a)>0\), o, lo que es lo mismo, \(f(b)>f(a)\). Es decir, \(f\) sería creciente respecto a los puntos \(a\) y \(b\). Aplicando el teorema en subintervalos, llegamos fácilmente al resultado.