2.6. Método de dicotomía#

2.6.1. Algoritmo#

Consideramos una función \(f:[a,b]\rightarrow\mathbb{R}\), continua en \([a,b]\), con \(f(a)\,f(b)<0\).

Es decir, estamos considerando una función que cumple las hipótesis del Teorema de Bolzano, por lo que ya sabemos que existe una raíz para \(f\) en el intervalo \([a,b]\). Una vez que sabemos que existe raíz el siguiente paso sería calcularla. Esto no siempre es sencillo (casi nunca, de hecho), y en algunos casos es directamente imposible. Entonces surge una segunda opción: aproximar esa raíz mediante un método numérico.

Llegados a este punto, hay distintos métodos numéricos que nos permiten aproximar la raíz de una función. Vamos a explicar ahora el más sencillo de ellos: el método de dicotomía, también conocido como método de bisección. En el siguiente capítulo explicaremos el método de Newton-Raphson, más eficiente numéricamente.

Para aproximar una raíz de \(f\) en \([a,b]\), mediante dicotomía, la idea es muy sencilla: vamos dividiendo el intervalo a la mitad y nos quedamos con la mitad en la que se cumplan las hipótesis de Bolzano. Es decir:

  • Dividimos el intervalo dado a la mitad.

  • Tomamos el punto medio del intervalo, \(c\), como aproximación de la raíz.

  • Comprobamos cuál de los 2 subintervalos que nos quedan (\([a,c]\) o \([c,b]\)) cumple la hipótesis de Bolzano.

  • Repetimos el proceso.

Si lo escribimos de forma más cercana a cómo lo programaremos, llegamos al algoritmo de dicotomía:

  • Inicializar \(\, [a_1,b_1]=[a,b]\).

  • Para \(\,k=1,2,\ldots, N_{\text{max}}\):

    • Calcular \(\,x_k=\displaystyle\frac{a_k+b_k}{2}\).

    • Si \(\, f(a_k)\,f(x_k)<0\), actualizar \([a_{k+1},b_{k+1}]=[a_k,x_k]\).

    • Si no, \([a_{k+1},b_{k+1}]=[x_k,b_k]\).

    • Realizamos un test de parada. Si se cumple, detenemos el algoritmo.

  • Continuamos iterando.

En cuanto al test de parada, lo más habitual es realizarlo en función de la diferencia relativa entre 2 iteraciones consecutivas. Sería algo así, para un parámetro de tolerancia, \(tol\), generalmente indicado por el usuario:

\[ \text{Si} \qquad \frac{\left| x_{k}-x_{k-1} \right|}{\left| x_{k} \right|} < tol \quad \Longrightarrow \quad \text{STOP}. \]

Theorem (Estimación del error )

Sea \(f:[a,b]\rightarrow\mathbb{R}\) una función continua en \([a,b]\) tal que \(f(a)\,f(b)<0\). Sea \(\alpha\in(a,b)\) tal que \(f(\alpha)=0\). Entonces, al aplicar el método de dicotomía en el intervalo \([a,b]\), el error máximo cometido en el paso \(k\) está acotado mediante la siguiente fórmula:

\[ |x_k - \alpha | \leq \frac{b-a}{2^k}. \]

Nosotros seguimos, mostrándoos cómo programar este algoritmo en Numpy.

De momento, lo escribiremos de forma directa, tal como lo hemos hecho en el algoritmo. Más adelante veremos cómo aislar parte o todo el algoritmo en una function, lo que nos permitirá realizar una programación estructurada.

import numpy as np
import sympy as sp

x = sp.symbols('x', real=True) # define la variable simbólica x
f_expr = sp.cos(x)
f = sp.Lambda(x,f_expr)

N_max = 100
tol = 1.e-5
a = 0.
b = 2.

x_aprox = np.zeros(N_max)

for k in range(0,N_max):
  x_aprox[k] = (a+b) / 2
  
  if f(x_aprox[k]) == 0: break
        
  if f(a) * f(x_aprox[k]) < 0:
     b = x_aprox[k]
  else:
     a = x_aprox[k]

  if ( (k > 0) and (np.abs(x_aprox[k]-x_aprox[k-1]) / np.abs(x_aprox[k]) < tol) ): break

print('Número de iteraciones realizadas: ', k+1) # Contamos 1 más porque empezamos el bucle en 0
print('Aproximación de la raíz: ', x_aprox[k])
    

Número de iteraciones realizadas:  17
Aproximación de la raíz:  1.5707855224609375

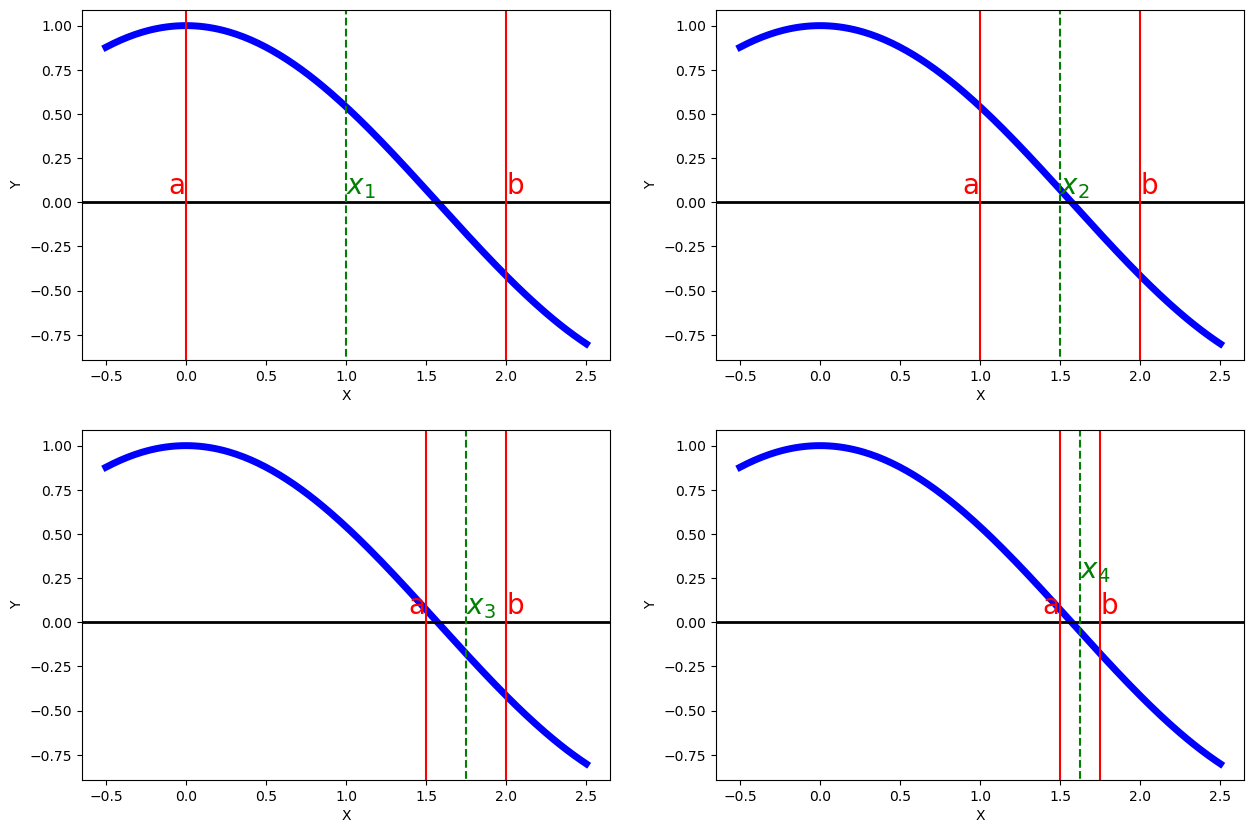
Vamos a representar gráficamente los primeros pasos del algoritmo en este caso:

import matplotlib as mp
import matplotlib.pyplot as plt
mp.__version__

%matplotlib inline

# Creamos gráficos de funciones
x1 = np.linspace(-0.5, 2.5, 200)
y1 = np.cos(x1)

fig, axs = plt.subplots(2, 2, figsize=(15,10))

ax1 = axs[0,0]
ax1.plot(x1, y1, c='b', lw='5')
ax1.set_ylabel('Y', fontsize=10)
ax1.set_xlabel('X', fontsize=10)
ax1.axhline(y=0., c='black', lw='2')

ax1.axvline(x=0., ymin=-1, ymax=1, c='r')
ax1.text(-0.11, 0.05, 'a', c='r', fontsize=20)
ax1.axvline(x=2., ymin=-1, ymax=1, c='r')
ax1.text(2, 0.05, 'b', c='r', fontsize=20)
ax1.axvline(x=1., ymin=-1, ymax=1, c='g', ls='--')
ax1.text(1, 0.05, '$x_1$', c='g', fontsize=20)

ax2 = axs[0,1]
ax2.plot(x1, y1, c='b', lw='5')
ax2.set_ylabel('Y', fontsize=10)
ax2.set_xlabel('X', fontsize=10)
ax2.axhline(y=0., c='black', lw='2')

ax2.axvline(x=1., ymin=-1, ymax=1, c='r')
ax2.text(0.89, 0.05, 'a', c='r', fontsize=20)
ax2.axvline(x=2., ymin=-1, ymax=1, c='r')
ax2.text(2, 0.05, 'b', c='r', fontsize=20)
ax2.axvline(x=1.5, ymin=-1, ymax=1, c='g', ls='--')
ax2.text(1.5, 0.05, '$x_2$', c='g', fontsize=20)

ax3 = axs[1,0]
ax3.plot(x1, y1, c='b', lw='5')
ax3.set_ylabel('Y', fontsize=10)
ax3.set_xlabel('X', fontsize=10)
ax3.axhline(y=0., c='black', lw='2')

ax3.axvline(x=1.5, ymin=-1, ymax=1, c='r')
ax3.text(1.39, 0.05, 'a', c='r', fontsize=20)
ax3.axvline(x=2., ymin=-1, ymax=1, c='r')
ax3.text(2, 0.05, 'b', c='r', fontsize=20)
ax3.axvline(x=1.75, ymin=-1, ymax=1, c='g', ls='--')
ax3.text(1.75, 0.05, '$x_3$', c='g', fontsize=20)

ax4 = axs[1,1]
ax4.plot(x1, y1, c='b', lw='5')
ax4.set_ylabel('Y', fontsize=10)
ax4.set_xlabel('X', fontsize=10)
ax4.axhline(y=0., c='black', lw='2')

ax4.axvline(x=1.5, ymin=-1, ymax=1, c='r')
ax4.text(1.39, 0.05, 'a', c='r', fontsize=20)
ax4.axvline(x=1.75, ymin=-1, ymax=1, c='r')
ax4.text(1.75, 0.05, 'b', c='r', fontsize=20)
ax4.axvline(x=1.625, ymin=-1, ymax=1, c='g', ls='--')
ax4.text(1.625, 0.25, '$x_4$', c='g', fontsize=20)

plt.show()
../../_images/06.Dicotomia_3_0.png

2.6.3. Ejercicio para que hagáis#

Utiliza el método de dicotomía para aproximar la raíz de la función \(f(x) = \ln\left(\tan(x)\right)\) en el intervalo \([0.1,1]\).

# ESCRIBE AQUÍ TU CÓDIGO

2.6.4. Ejercicios para practicar un poco más#

Para practicar un poco sobre lo que se explica en este tema os recomendamos los siguientes ejercicios del maravilloso blog https://existelimite.blogspot.com/, aunque es posible que en ellos encuentres algunas cosas (sobre la unicidad de raíces con el Teorema de Rolle, sobre todo), que aún no os hayamos contado: