4.2. Integración de Riemann#

Sea un intervalo \([a,b] \subset \mathbb R\) y sea \(\,f : [a,b] \longrightarrow \mathbb R\) una función acotada.

En primer lugar, definimos el concepto de partición:

Definition (Partición de un intervalo)

Se llama partición \(\mathcal{P}\) de \([a,b]\) a un conjunto de puntos \( \left\{ x_0, x_1, \ldots, x_n \right\} \) que verifica:

\[ a = x_0 < x_1 < x_2 < \ldots < x_{n-1} < x_n = b. \]

Dada una partición \(\mathcal P\), denotamos

\[M_i = \underset{x_{i-1} \leq x \leq x_i}{\sup} f(x),\]
\[m_i = \underset{x_{i-1} \leq x \leq x_i}{\inf} f(x).\]

4.2.1. Sumas de Riemann#

Definition (Sumas de Riemann)

  • Se llama suma superior de Riemann de la función \(f\) relativa a la partición \(\mathcal P\) a:

    \[ U (\mathcal P,f) = \overset{n}{\underset{i=1}{\sum}} \, M_i (x_i - x_{i-1}). \]

  • Se llama suma inferior de Riemann de la función \(f\) relativa a la partición \(\mathcal P\) a:

    \[ L (\mathcal P,f) = \overset{n}{\underset{i=1}{\sum}} \, m_i (x_i - x_{i-1}). \]
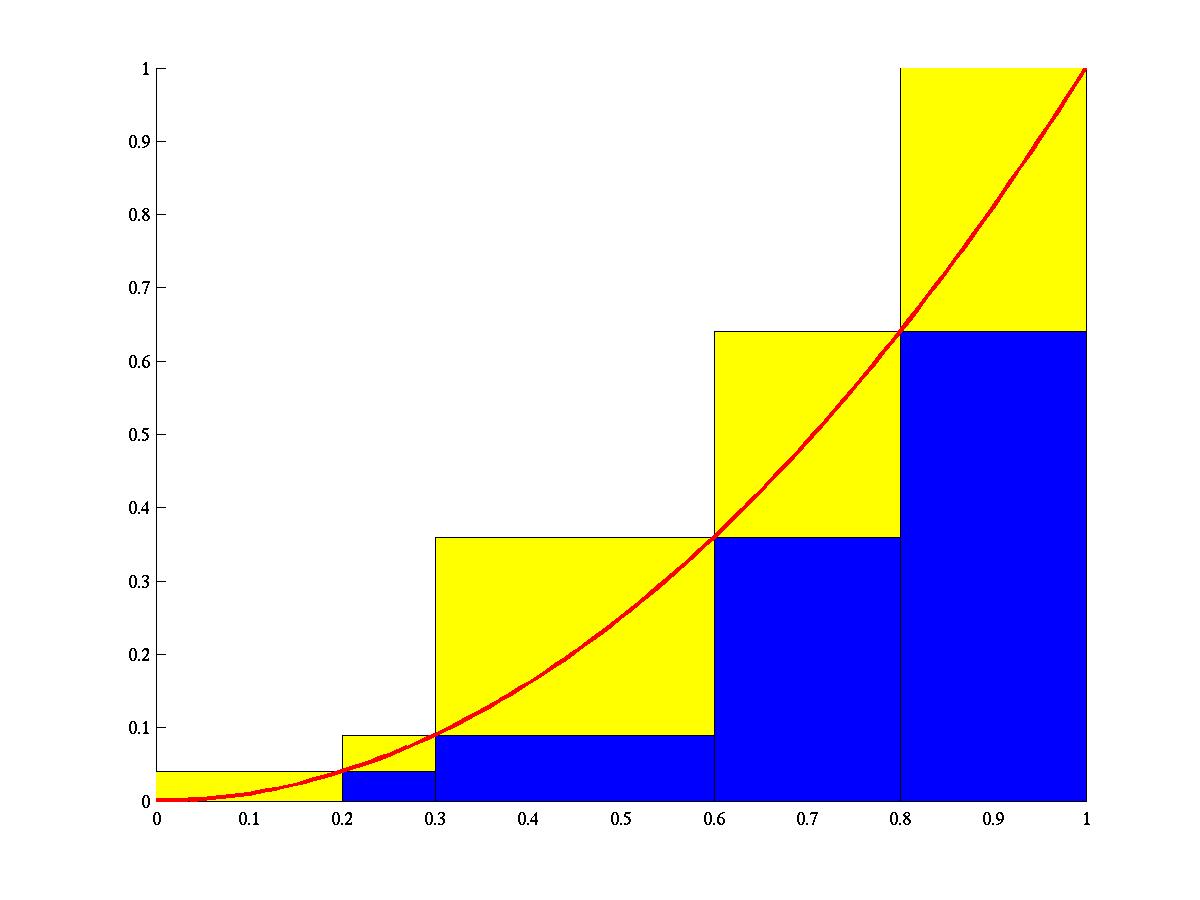
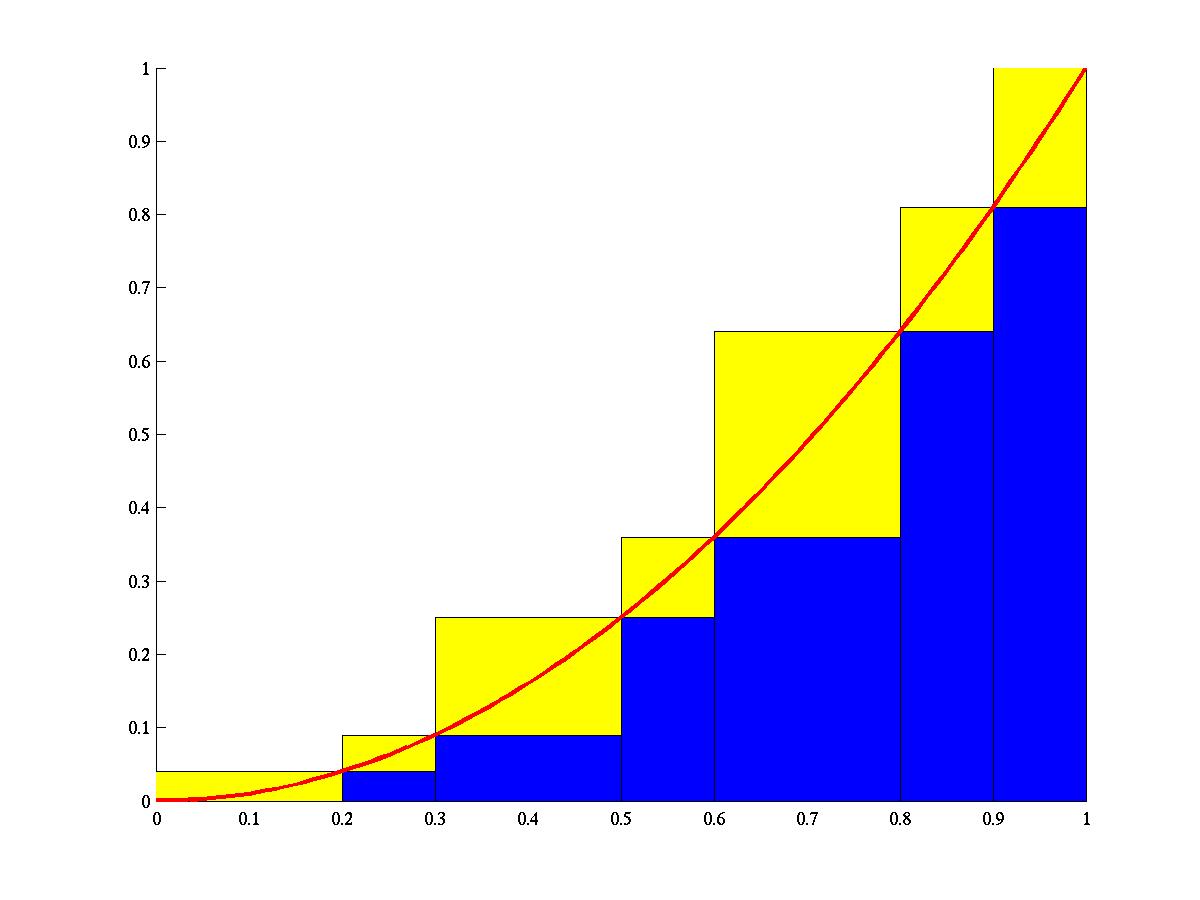
../../_images/cap_4_trc_riemann2.jpg ../../_images/cap_4_trc_riemann3.jpg

Example

Dada la partición \(\mathcal{P} = \left\{0, \frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3}, \frac{\pi}{2}, \pi \right\}\) en el intervalo \([0,\pi]\) y la función \(f(x)=\sin x\), calcula la suma superior de Riemann \(U (\mathcal P,f)\).

Solución:

Representamos gráficamente la función seno en el intervalo \([0,\pi]\) y la partición \(\mathcal{P}\) con Matplotlib:

import numpy as np
import matplotlib as mp
import matplotlib.pyplot as plt

xx = np.linspace(0, np.pi, 200)
yy = np.sin(xx)

x0=0; x1=np.pi/6; x2=np.pi/4; x3=np.pi/3; x4=np.pi/2; x5=np.pi

fig = plt.figure(figsize = (10,5))
#plt.ylim(-5,20)

plt.plot(xx, yy, c='r', lw='5', label = '$f=\sin(x)$')
plt.ylabel('Y', fontsize=10)
plt.xlabel('X', fontsize=10)
plt.axhline(y=0., c='black', lw='2')
plt.axvline(x=x0, c='black', lw='2', ls=':')
plt.text(x0, 0.1, '$x_{0}=a$', c='b', fontsize=20)
plt.axvline(x=x1, c='black', lw='2', ls=':')
plt.text(x1, 0.05, '$x_{1}$', c='b', fontsize=20)
plt.axvline(x=x2, c='black', lw='2', ls=':')
plt.text(x2, 0.05, '$x_{2}$', c='b', fontsize=20)
plt.axvline(x=x3, c='black', lw='2', ls=':')
plt.text(x3, 0.05, '$x_{3}$', c='b', fontsize=20)
plt.axvline(x=x4, c='black', lw='2', ls=':')
plt.text(x4, 0.05, '$x_{4}$', c='b', fontsize=20)
plt.axvline(x=x5, c='black', lw='2', ls=':')
plt.text(x5, 0.1, '$x_{5}=b$', c='b', fontsize=20)

plt.show()
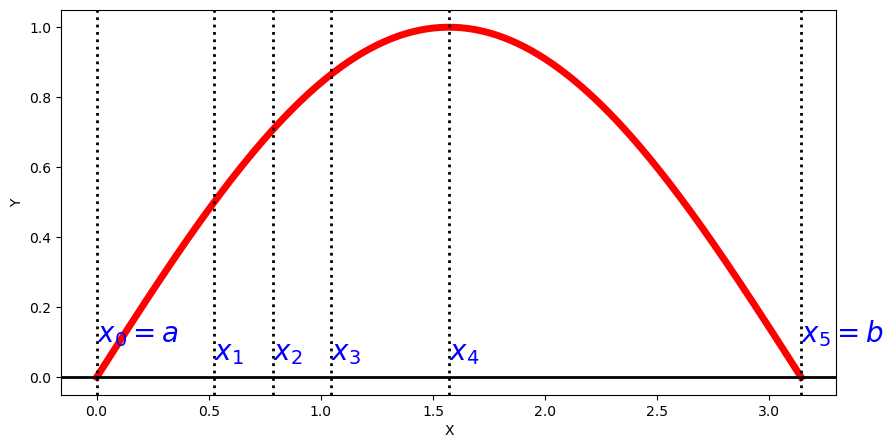
../../_images/02.IntegracionRiemann_7_0.png

Vemos que la función \(\sin x\) es creciente en el intervalo \([0,\frac{\pi}{2}]\) y decreciente en \([\frac{\pi}{2},\pi]\), por lo que:

  • \(\max\left\{\sin(x), x\in[0,\frac{\pi}{6}]\right\}=\sin\left(\frac{\pi}{6}\right)=\frac12\),

  • \(\max\left\{\sin(x), x\in[\frac{\pi}{6},\frac{\pi}{4}]\right\}=\sin\left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\),

  • \(\max\left\{\sin(x), x\in[\frac{\pi}{4},\frac{\pi}{3}]\right\}=\sin\left(\frac{\pi}{3}\right)=\frac{\sqrt{3}}{2}\),

  • \(\max\left\{\sin(x), x\in[\frac{\pi}{3},\frac{\pi}{2}]\right\}=\sin\left(\frac{\pi}{2}\right)=1\),

  • \(\max\left\{\sin(x), x\in[\frac{\pi}{2},\pi]\right\}=\sin\left(\frac{\pi}{2}\right)=1\).

Por tanto:

\[\begin{eqnarray*} U (\mathcal P,f) &=& \left(\frac{\pi}{6} - 0\right) \frac12 + \left(\frac{\pi}{4} - \frac{\pi}{6}\right) \frac{\sqrt{2}}{2} + \left(\frac{\pi}{3} - \frac{\pi}{4}\right) \frac{\sqrt{3}}{2} + \left(\frac{\pi}{2} - \frac{\pi}{3}\right) 1 + \\ && + \left(\pi- \frac{\pi}{2}\right) 1 = \frac{18+\sqrt{2}+\sqrt{3}}{24}\pi \approx 2.7680. \end{eqnarray*}\]

4.2.2. Definición de integrabilidad de Riemann#

Definition

Dada una función \(f\) acotada, se dice que \(f\) es integrable en \([a,b]\) en el sentido de Riemann si y sólo si:

\[ \forall \varepsilon > 0 , \quad \exists \mathcal P \text{ partición de $[a,b]$ tal que } \, U(\mathcal P,f) - L(\mathcal P,f) < \varepsilon. \]

Se escribe \(f\in{\cal R}[a,b]\).

Interpretación geométrica:

Si \(f(x)\) es una función positiva en un intervalo \([a,b]\), su integral de Riemann, \(\displaystyle\int_a^bf(x)\,dx\), representa el área limitada por la curva \(y = f(x)\), el eje \(y = 0\) y las rectas \(x = a\) y \(x = b\).

Example

Calcule \(\int_{-3}^3 \sqrt{9-x^2} dx\).

Solución:

Dibujemos la función \(\sqrt{9-x^2}\) en el intervalo \([-3,3]\) con Sympy:

p = sp.plot(sp.sqrt(9-x**2), (x, -3, 3), show=False)
p.line_color='r'
p.xlabel='x'
p.ylabel='y'
p.legend=True
p.show()
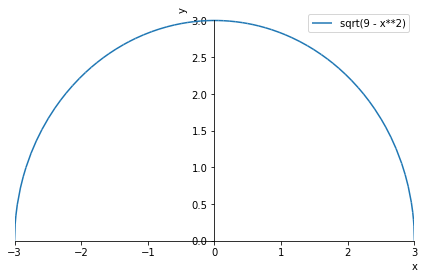
../../_images/02.IntegracionRiemann_10_0.png

Vemos que en el intervalo \([-3,3]\) la función define una semicircunferencia de radio 3. Sabemos por geometría que el área de una circunferencia es \(A = \pi r^2 = \pi \, 3^2 = 9 \pi\). Así, el área de la semicircunferencia es \(\frac{9\pi}{2}\), luego

\[\int_{-3}^3 \sqrt{9-x^2} dx=\frac{9\pi}{2}.\]

4.2.3. Propiedades de la integral de Riemann#

Property (Integrabilidad según Riemann)

  1. Toda función continua en \([a,b]\) es integrable en \([a,b]\) (es decir: \(f\in\mathcal{C}^{0}[a,b]\Rightarrow f\in\mathcal{R}[a,b]\)). En consecuencia, toda función derivable es integrable.

  2. Toda función monótona y acotada en \([a,b]\) es integrable en \([a,b]\).

  3. Toda función acotada en \([a,b]\) que presenta en dicho intervalo un número finito de puntos de discontinuidad, es integrable en \([a,b]\).

  4. Sea \(f\) una función integrable en \([a,b]\) en el sentido de Riemann, y tal que:

    \[m \leq f(x) \leq M , \quad \forall x \in [a,b].\]

    Si \(g\) es continua en \([m,M]\), entonces la función compuesta \(g \circ f\) es integrable en \([a,b]\).

Property (Propiedades aritméticas de la integración de Riemann)

Sean \(f, g \in {\cal R}[a,b]\). Entonces:

  • \(\forall \alpha \in \mathbb R\), \(\alpha f\in {\cal R}[a,b]\), y se cumple:

    \[ \int_a ^b (\alpha\, f)(x) \,dx = \alpha \int_a ^b f(x) \,dx. \]

  • \(f \pm g \in {\cal R}[a,b]\) y se cumple:

    \[ \int_a ^b (f \pm g)(x) \,dx = \int_a ^b f(x) \,dx \pm \int_a ^b g(x) \,dx. \]

  • \(fg \in {\cal R}[a,b]\).

Property (Aditividad en intervalos)

Sea \(f \in {\cal R}[a,b]\) y supongamos un punto \(c\) en el intervalo \((a,b)\) (es decir, \(a < c < b\)).

Entonces \(f \in {\cal R}[a,c]\) y \(f \in {\cal R}[c,b]\), y se verifica:

\[\int_a ^b f(x)\,dx = \int_a ^c f(x) \,dx + \int_c ^b f(x) \,dx.\]

Property (Acotaciones)

Sean \(f, g \in {\cal R}[a,b]\).

  • Si \(f \leq g\) en \([a,b]\), entonces \(\displaystyle\int_a ^b f(x) \,dx \leq \int_a ^b g(x) \,dx\).

  • Si \(m\leq f(x) \leq M\), \(\forall x \in [a,b]\), entonces

    \[m(b-a)\leq \int_a ^b f(x) \,dx \leq M (b - a).\]

  • \(|f| \in {\cal R}[a,b]\), y se cumple:

    \[ | \int_a^b f(x) \,dx | \leq \int_a^b |f(x)|\,dx. \]

4.2.4. Algunos enlaces para ir más allá#

Si te ha picado la curiosidad y quieres ampliar tus conocimientos sobre la integral de Riemann, aquí tienes algunos enlaces que nos parecen interesantes:

  • En la página de Silvestre Paredes Hernández, profesor en la Universidad Politécnica de Cartagena, encontramos este capítulo completo con todo lo que necesitáis saber sobre la integral de Riemann, teorema fundamental del cálculo, integración impropia y aplicaciones de la integral: https://www.dmae.upct.es/~paredes/mat1giqi/apuntes/Tema12.pdf.

  • De la página personal de Jesús María Sánchez Montero, profesor en la Universidad de Sevilla: https://personal.us.es/jsmonter/jes1/pdf/intedef.pdf. Un pdf gráficamente muy chulo, con ejercicios resueltos e información ampliada.

  • En la página de Benito J. González Rodríguez, profesor de la Universidad de La Laguna, encontramos el siguiente documento, que contiene una introducción muy completa sobre la integración de Riemann: https://bjglez.webs.ull.es/06-integral.pdf. Podéis ver, por ejemplo, la demostración de que las funciones monótonas son Riemann-integrables.