3.3. Derivadas sucesivas

Vamos a suponer que tenemos una función \(f:(a,b) \longrightarrow \mathbb R\), derivable en \((a,b)\). Podemos considerar, entonces, su función derivada en \((a,b)\):

\[\begin{equation*} \begin{array}{cccc} f': & (a,b) & \longrightarrow & \mathbb{R} \\ & x & \leadsto & f'(x) \end{array} \end{equation*}\]

Definition

Dado un punto \(x_0 \in (a,b)\) definimos la derivada segunda de \(f\) en \(x_0\) como la derivada de \(f'\) en \(x_0\), es decir, como el siguiente límite:

\[\begin{equation*} f''(x_0) =(f')'(x_0) = \lim_{h\rightarrow 0} \dfrac{f'(x_0+h) - f'(x_0)}{h}. \end{equation*}\]

Si este límite existe y es finito, se dice que \(f\) es derivable dos veces en \(x_0\).

Definition

Si \(f\) admite derivada segunda en todo punto de \((a,b)\) definimos su derivada tercera en \(x_0\) como el límite, si existe,

\[\begin{equation*} f'''(x_0) =(f'')'(x_0) = \lim_{h\rightarrow 0} \dfrac{f''(x_0+h) - f''(x_0)}{h}. \end{equation*}\]

Así podríamos definir la derivada cuarta, etc. En general, una vez que se tiene \(f^{n-1}:(a,b) \longrightarrow \mathbb R\), definimos la derivada n-ésima en \(x_{0}\) como:

\[\begin{equation*} f^{n}(x_0) = \left( f^{(n-1)}\right)'(x_0). \end{equation*}\]

Por ejemplo, si partimos de una función sencilla,

• \(f(x) = \sin(x)+x^2\),

• \(f'(x) = \cos(x) + 2x\),

• \(f''(x) = -\sin(x) + 2\),

• \(f'''(x) = - \cos(x)\),

• etc.

La orden en Sympy para calcular la derivada n-ésima de una expresión es la siguiente:

import sympy as sp

x = sp.symbols('x', real=True)
f_exp = sp.sin(x) + x**2
display(f_exp)
display(sp.diff(f_exp,x))
display(sp.diff(f_exp,x,2))
display(sp.diff(f_exp,x,3))
# Nota: también se puede usar la siguiente escritura:
# display(f_exp.diff(x,3))

\[\displaystyle x^{2} + \sin{\left(x \right)}\]

\[\displaystyle 2 x + \cos{\left(x \right)}\]

\[\displaystyle 2 - \sin{\left(x \right)}\]

\[\displaystyle - \cos{\left(x \right)}\]

Definition (Clase de una función)

Sea \(f:(a,b) \longrightarrow \mathbb R\). Diremos que

1. \(f\) es de clase \(n\) en \((a,b)\), \(f \in \mathcal{C}^n(a,b)\), si existen las \(n\) primeras derivadas de \(f\), \(f'\), \(f''\), \(\ldots\), \(f^{(n}\), y además \(f^{(n}\) es una función continua,

2. \(f\) es de clase \(0\) en \((a,b)\), \(f\in\mathcal{C}^0(a,b)\), si \(f\) es continua,

3. \(f\) es de clase \(\infty\) en (a,b), \(f \in \mathcal{C}^\infty(a,b)\), si \(f\in\mathcal{C}^n(a,b), \forall n\in\mathbb N\),

4. \(f\) es de clase \(n\) en \([a,b]\), \(f \in \mathcal{C}^n[a,b]\),si existe \((c,d)\supset [a,b]\) tal que \(f\in\mathcal{C}^n(c,d)\).

Veamos un ejercicio/ejemplo completo para practicar:

Example

Sea la función \(f(x) = \dfrac{1}{2} x |x|\), \(\forall x\in\mathbb R\). ¿Cuál es la clase de \(f\) en \(\mathbb R\)?

Respuesta: En primer lugar, separamos el valor absoluto según lo de dentro sea positivo o negativo,

\[\begin{split} f(x)=\left\{ \begin{array}{cl} -\frac{1}{2}x^2&\quad\mbox{si }x<0, \\ \frac{1}{2}x^2&\quad\mbox{si }x\geq 0. \end{array}\right. \end{split}\]

La representación gráfica de \(f\) en Sympy se puede obtener del siguiento modo:

f_expr = 0.5*x*sp.Abs(x)
p = sp.plot(f_expr, (x, -4, 4), show=False)
p[0].line_color='r'
p.xlabel='x'
p.ylabel='y'
p.show()

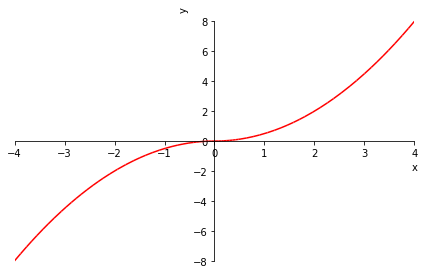
Ahora vamos a comprobar si \(f\) es una función continua. Es evidente que \(f\) es continua en todo punto \(x\) distinto del \(0\), ya que para \(x<0\) y para \(x>0\) \(f\) es un polinomio. El \(0\) es un punto que debemos estudiar con más cuidado, ya que en él se produce un cambio en la definición de \(f\). Calculamos sus límites laterales,

\[\begin{eqnarray*} &&\lim_{x\to 0^{-}}f(x)=\lim_{x\to 0^{-}}-\frac{1}{2}x^2=0=f(0), \\ &&\lim_{x\to 0^{+}}f(x)=\lim_{x\to 0^{+}}\frac{1}{2}x^2=0=f(0). \end{eqnarray*}\]

Como los dos límites coinciden con el valor de la función en ese punto, ya sabemos que \(f\) es continua en \(0\) y, por tanto, continua en todo \(\mathbb R\). Entonces

\[\fbox{$f\in\mathcal{C}^0(\mathbb R).$}\]

f = sp.Lambda(x, f_expr)
display(sp.limit(f(x),x,0,dir='-'))
display(sp.limit(f(x),x,0,dir='+'))
print('f es de clase 0?', sp.limit(f(x),x,0) == f(0))

\[\displaystyle 0\]

\[\displaystyle 0\]

f es de clase 0? True

Vamos a calcular ahora la derivada de \(f\). El \(0\) es el punto problemático. Estudiamos \(f'(0)\) en primer lugar, calculando sus derivadas laterales:

\[\begin{eqnarray*} &&f'(0^{-})=\lim_{h\to 0^{-}}\frac{f(h)-f(0)}{h}=\lim_{h\to 0^{-}}\frac{-\frac{1}{2}h^2-0}{h}=\lim_{h\to 0^{-}}-\frac{1}{2}h^2=0, \\ &&f'(0^{+})=\lim_{h\to 0^{+}}\frac{f(h)-f(0)}{h}=\lim_{h\to 0^{+}}\frac{\frac{1}{2}h^2-0}{h}=\lim_{h\to 0^{+}}\frac{1}{2}h^2=0. \end{eqnarray*}\]

Como las derivadas laterales coinciden, sabemos que \(f'\) es una función derivable en el \(0\) y que \(f'(0)=0\). En el resto de puntos es muy sencillo derivar, porque \(f\) es un polinomio. Resulta entonces,

\[\begin{split} f'(x)=\left\{ \begin{array}{cl} -x&\quad\mbox{si }x<0, \\ 0&\quad\mbox{si }x=0, \\ x&\quad\mbox{si }x\geq 0. \end{array}\right. \end{split}\]

Es muy sencillo comprobar que \(f'\) es una función continua. Entonces

\[\fbox{$f\in\mathcal{C}^1(\mathbb R).$}\]

La representación gráfica de \(f'\) se obtiene del siguiente modo.

p = sp.plot(f_expr.diff(x,1), (x, -4, 4), show=False)
p[0].line_color='r'
p.xlabel='x'
p.ylabel='y'
p.show()

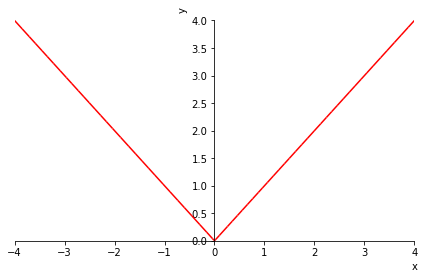
Ahora intentamos calcular la derivada segunda de \(f\). Comenzamos con el punto problemático, \(x=0\), calculando sus derivadas laterales.

\[\begin{eqnarray*} &&f''(0^{-})=\lim_{h\to 0^{-}}\frac{f'(h)-f'(0)}{h}=\lim_{h\to 0^{-}}\frac{-h-0}{h}=\lim_{h\to 0^{-}}-1=-1, \\ &&f''(0^{+})=\lim_{h\to 0^{+}}\frac{f'(h)-f'(0)}{h}=\lim_{h\to 0^{+}}\frac{h-0}{h}=\lim_{h\to 0^{+}}1=1. \end{eqnarray*}\]

Como las derivadas laterales no coinciden, resulta que \(\not\exists f''(0)\). Por lo tanto

\[\fbox{$f\not\in\mathcal{C}^2(\mathbb R).$}\]

Con la ayuda de Sympy podríamos analizarlo del siguiente modo:

f1_expr = f_expr.diff(x,1)
f1 = sp.Lambda(x, f1_expr)

h = sp.symbols('h', real=True)
f2_0Minus = sp.limit((f1(h)-f1(0))/h,h,0,dir='-')
f2_0Plus = sp.limit((f1(h)-f1(0))/h,h,0,dir='+')
print('f2_0Minus = ', f2_0Minus, ', f2_0Plus = ', f2_0Plus) 
print('Existe f\'\'(0)?',f2_0Minus==f2_0Plus)

f2_0Minus =  -1.00000000000000 , f2_0Plus =  1.00000000000000
Existe f''(0)? False